9 Memvisualisasikan banyak distribusi sekaligus
Ada banyak skenario di mana kami ingin memvisualisasikan beberapa distribusi sekaligus. Misalnya, pertimbangkan data cuaca. Kami mungkin ingin memvisualisasikan bagaimana suhu bervariasi di bulan yang berbeda sementara juga menunjukkan distribusi suhu yang diamati dalam setiap bulan. Skenario ini mengharuskan menunjukkan dua belas distribusi suhu sekaligus, satu untuk setiap bulan. Tak satu pun dari visualisasi yang dibahas dalam Bab 7 atau 8berfungsi dengan baik dalam kasus ini. Sebaliknya, pendekatan yang layak termasuk plot kotak, plot biola, dan plot ridgeline.
Setiap kali kita berurusan dengan banyak distribusi, akan sangat membantu untuk memikirkan variabel respon dan satu atau lebih variabel pengelompokan. Variabel respons adalah variabel yang distribusinya ingin kami tampilkan. Variabel pengelompokan menentukan himpunan bagian dari data dengan distribusi yang berbeda dari variabel respons.Misalnya, untuk distribusi suhu lintas bulan, variabel respons adalah suhu dan variabel pengelompokan adalah bulan.Semua teknik yang dibahas dalam bab ini menggambarkan variabel respons di sepanjang satu sumbu dan variabel pengelompokan di sepanjang lainnya. Berikut ini, pertama saya akan menggambarkan pendekatan yang menunjukkan variabel respon sepanjang sumbu vertikal, dan kemudian saya akan menjelaskan pendekatan yang menunjukkan variabel respon di sepanjang sumbu horizontal. Dalam semua kasus yang dibahas, kita bisa membalik sumbu dan sampai pada alternatif dan visualisasi yang layak. Saya menunjukkan di sini bentuk kanonik dari berbagai visualisasi.
9.1 Memvisualisasikan distribusi sepanjang sumbu vertikal
Pendekatan paling sederhana untuk menunjukkan banyak distribusi sekaligus adalah dengan menunjukkan rata-rata atau mediannya sebagai poin, dengan beberapa indikasi variasi di sekitar rata-rata atau median yang ditunjukkan oleh bar kesalahan. Gambar 9.1 menunjukkan pendekatan ini untuk distribusi suhu bulanan di Lincoln, Nebraska, pada 2016. Saya telah memberi label angka ini sebagai buruk karena ada beberapa masalah dengan pendekatan ini.Pertama, dengan merepresentasikan setiap distribusi hanya dengan satu titik dan dua bilah galat, kami kehilangan banyak informasi tentang data. Kedua, tidak segera jelas apa yang direpresentasikan oleh poin-poin tersebut, meskipun sebagian besar pembaca mungkin akan menebak bahwa mereka mewakili mean atau median. Ketiga, jelas tidak jelas apa yang diwakili bilah galat. Apakah mereka mewakili standar deviasi data, kesalahan standar rata-rata, interval kepercayaan 95%, atau yang lainnya? Tidak ada standar yang diterima secara umum. Dengan membaca keterangan gambar pada Gambar 9.1 , kita dapat melihat bahwa mereka mewakili di sini dua kali standar deviasi dari suhu rata-rata harian, dimaksudkan untuk menunjukkan kisaran yang berisi sekitar 95% dari data. Namun, bar kesalahan lebih umum digunakan untuk memvisualisasikan kesalahan standar (atau dua kali kesalahan standar untuk interval kepercayaan 95%), dan mudah bagi pembaca untuk mengacaukan kesalahan standar dengan standar deviasi. Kesalahan standar mengkuantifikasi seberapa akurat perkiraan kami tentang rata-rata, sedangkan standar deviasi memperkirakan berapa banyak penyebaran dalam data di sekitar rata-rata.Dimungkinkan untuk dataset memiliki kesalahan standar sangat kecil dari rata-rata dan standar deviasi yang sangat besar. Keempat, bar kesalahan simetris menyesatkan jika ada kemiringan dalam data, yang terjadi di sini dan hampir selalu untuk dataset dunia nyata.

Gambar 9.1: Suhu rata-rata harian di Lincoln, Nebraska pada 2016. Poin mewakili rata-rata suhu harian rata-rata setiap bulan, rata-rata sepanjang hari dalam sebulan, dan bar kesalahan mewakili dua kali standar deviasi dari suhu rata-rata harian dalam setiap bulan. Angka ini telah dilabeli sebagai "buruk" karena karena bar kesalahan secara konvensional digunakan untuk memvisualisasikan ketidakpastian estimasi, bukan variabilitas dalam suatu populasi. Sumber data: Weather Underground
Kami dapat mengatasi keempat kekurangan pada Gambar 9.1 dengan menggunakan metode tradisional dan umum digunakan untuk memvisualisasikan distribusi, boxplot.Boxplot membagi data menjadi kuartil dan memvisualisasikannya secara standar (Gambar 9.2 ).

Gambar 9.2: Anatomi plot. Yang ditunjukkan adalah awan titik (kiri) dan plot kotak yang sesuai (kanan). Hanya nilai y dari titik-titik yang divisualisasikan dalam boxplot. Garis di tengah-tengah plot kotak mewakili median, dan kotak melingkupi 50% tengah dari data. Kumis atas dan bawah memanjang ke maksimum dan minimum data atau ke maksimum atau minimum yang jatuh dalam 1,5 kali tinggi kotak, mana yang menghasilkan kumis pendek.Jarak 1,5 kali tinggi kotak di kedua arah disebut pagar atas dan bawah.Poin data individual yang berada di luar pagar disebut sebagai outlier dan biasanya ditampilkan sebagai titik individual.
Boxplots sederhana namun informatif, dan mereka bekerja dengan baik ketika diplot berdampingan untuk memvisualisasikan banyak distribusi sekaligus. Untuk data suhu Lincoln, menggunakan boxplots mengarah ke Gambar 9.3 . Pada gambar itu, kita sekarang dapat melihat bahwa suhu sangat miring pada bulan Desember (sebagian besar hari cukup dingin dan beberapa sangat dingin) dan tidak terlalu miring sama sekali dalam beberapa bulan lain, misalnya pada bulan Juli.

Gambar 9.3: Suhu rata-rata harian di Lincoln, Nebraska, divisualisasikan sebagai plot-box.
Boxplots diciptakan oleh ahli statistik John Tukey pada awal 1970-an, dan mereka dengan cepat memperoleh popularitas karena sangat informatif dan mudah digambar dengan tangan. Kebanyakan visualisasi data diambil dengan tangan pada saat itu. Namun, dengan kemampuan komputasi dan visualisasi modern, kami tidak terbatas pada apa yang mudah digambar dengan tangan. Oleh karena itu, baru-baru ini, kita melihat plot kotak digantikan oleh plot biola, yang setara dengan perkiraan kepadatan yang dibahas pada Bab 7 tetapi diputar 90 derajat dan kemudian dicerminkan (Gambar 9.4 ).Biola dapat digunakan kapan saja orang akan menggunakan boxplot, dan mereka memberikan gambar yang jauh lebih bernuansa data. Secara khusus, plot biola akan secara akurat menampilkan data bimodal sedangkan boxplot tidak.

Gambar 9.4: Anatomi plot biola. Ditampilkan adalah awan titik (kiri) dan plot biola yang sesuai (kanan). Hanya nilai y poin yang divisualisasikan dalam plot biola. Lebar biola pada nilai y yang diberikan mewakili kerapatan titik pada nilai y itu . Secara teknis, plot biola adalah perkiraan kepadatan yang diputar 90 derajat dan kemudian dicerminkan. Oleh karena itu, biola simetris. Biola masing-masing dimulai dan diakhiri dengan nilai data minimum dan maksimum. Bagian paling tebal dari biola sesuai dengan kepadatan titik tertinggi dalam dataset.
Sebelum menggunakan biola untuk memvisualisasikan distribusi, verifikasi bahwa Anda memiliki cukup banyak titik data di masing-masing kelompok untuk membenarkan menunjukkan kerapatan titik sebagai garis halus.
Ketika kami memvisualisasikan data suhu Lincoln dengan biola, kami memperoleh Gambar 9.5 . Kita sekarang dapat melihat bahwa beberapa bulan memiliki data bimodal yang cukup. Sebagai contoh, bulan November tampaknya memiliki dua kelompok suhu, satu sekitar 50 derajat dan satu sekitar 35 derajat Fahrenheit.

Gambar 9.5: Suhu rata-rata harian di Lincoln, Nebraska, divisualisasikan sebagai plot biola.
Karena plot biola berasal dari perkiraan kepadatan, mereka memiliki kekurangan yang serupa (Bab 7 ). Secara khusus, mereka dapat menghasilkan tampilan bahwa ada data di mana tidak ada, atau bahwa kumpulan data sangat padat padahal sebenarnya sangat jarang. Kami dapat mencoba untuk menghindari masalah ini dengan hanya memplot semua titik data individual secara langsung, sebagai titik (Gambar 9.6 ). Sosok seperti itu disebut strip chart. Pada dasarnya, diagram garis baik-baik saja, selama kita memastikan bahwa kita tidak merencanakan terlalu banyak poin di atas satu sama lain. Solusi sederhana untuk overplotting adalah dengan menyebarkan titik-titik di sepanjang sumbu x , dengan menambahkan beberapa noise acak dalam dimensi x (Gambar 9.7 ). Teknik ini juga disebut jittering.
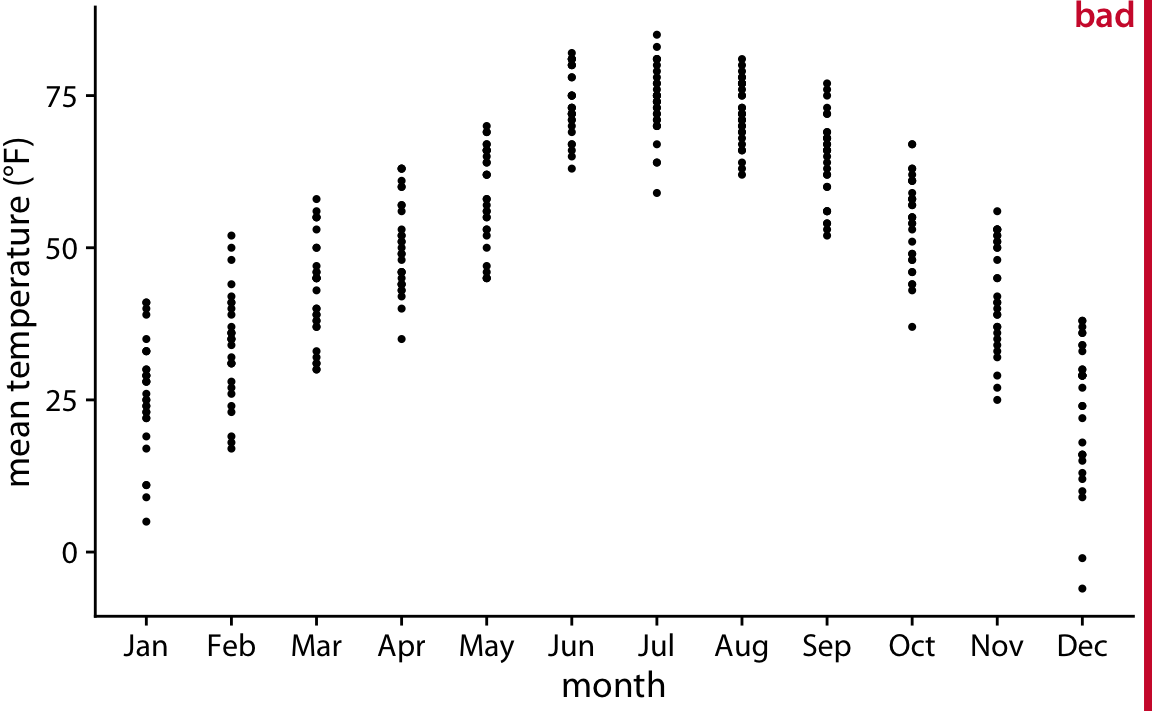
Gambar 9.6: Suhu rata-rata harian di Lincoln, Nebraska, divisualisasikan sebagai bagan garis. Setiap titik mewakili suhu rata-rata selama satu hari.Angka ini dilabeli sebagai "buruk" karena begitu banyak titik diplot satu sama lain sehingga tidak mungkin untuk memastikan suhu mana yang paling umum di setiap bulan.

Gambar 9.7: Suhu rata-rata harian di Lincoln, Nebraska, divisualisasikan sebagai bagan garis. Titik-titik telah dikocok sepanjang sumbu x untuk lebih menunjukkan kepadatan titik pada setiap nilai suhu.
Setiap kali dataset terlalu jarang untuk menjustifikasi visualisasi biola, memplot data mentah sebagai titik individual akan dimungkinkan.
Akhirnya, kita dapat menggabungkan yang terbaik dari kedua dunia dengan menyebarkan titik-titik secara proporsional dengan kerapatan titik pada koordinat y yang diberikan.Metode ini, disebut plot sina (Sidiropoulos et al. 2018 ) , dapat dianggap sebagai hibrida antara plot biola dan titik-titik jitter, dan ini menunjukkan setiap titik individu sambil juga memvisualisasikan distribusi. Di sini saya telah menggambar plot sina di atas biola untuk menyoroti hubungan antara kedua pendekatan ini (Gambar 9.8 ).

Gambar 9.8: Temperatur rata-rata harian di Lincoln, Nebraska, divisualisasikan sebagai plot sina (kombinasi poin individu dan biola). Titik-titik telah dikocok sepanjang sumbu x secara proporsional dengan kerapatan titik pada suhu masing-masing. Nama plot sina dimaksudkan untuk menghormati Sina Hadi Sohi, seorang mahasiswa di University of Copenhagen, Denmark, yang menulis versi pertama dari kode yang digunakan para peneliti di universitas untuk membuat plot seperti itu (Frederik O. Bagger, komunikasi pribadi).
9.2 Memvisualisasikan distribusi sepanjang sumbu horizontal
Dalam Bab 7 , kami memvisualisasikan distribusi sepanjang sumbu horisontal menggunakan histogram dan plot kepadatan. Di sini, kami akan memperluas ide ini dengan mengejutkan plot distribusi ke arah vertikal. Visualisasi yang dihasilkan disebut plot ridgeline, karena plot ini terlihat seperti ridgeline gunung. Plot Ridgeline cenderung bekerja dengan baik jika ingin menunjukkan tren dalam distribusi dari waktu ke waktu.
Plot ridgeline standar menggunakan estimasi kepadatan (Gambar 9.9 ). Ini sangat terkait erat dengan plot biola, tetapi sering membangkitkan pemahaman data yang lebih intuitif.Sebagai contoh, dua kelompok suhu sekitar 35 derajat dan 50 derajat Fahrenheit pada bulan November jauh lebih jelas pada Gambar 9.9 daripada pada Gambar 9.5 .

Gambar 9.9: Suhu di Lincoln, Nebraska, pada 2016, divisualisasikan sebagai plot ridgeline. Untuk setiap bulan, kami menunjukkan distribusi suhu rata-rata harian yang diukur dalam Fahrenheit. Konsep tokoh asli: Wehrwein ( 2017 ) .
Karena sumbu x menunjukkan variabel respons dan sumbu ymenunjukkan variabel pengelompokan, tidak ada sumbu terpisah untuk perkiraan kerapatan dalam plot ridgeline.Perkiraan kepadatan ditampilkan di samping variabel pengelompokan. Ini tidak berbeda dari plot biola, di mana kepadatan juga ditampilkan di samping variabel pengelompokan, tanpa skala eksplisit yang terpisah. Dalam kedua kasus, tujuan plot bukan untuk menunjukkan nilai kerapatan tertentu tetapi untuk memungkinkan perbandingan bentuk kerapatan dan ketinggian relatif antar kelompok secara mudah.
Pada prinsipnya, kita dapat menggunakan histogram alih-alih plot kerapatan dalam visualisasi ridgeline. Namun, angka yang dihasilkan seringkali tidak terlihat sangat baik (Gambar 9.10 ). Masalahnya mirip dengan histogram yang bertumpuk atau tumpang tindih (Bab 7 ). Karena garis-garis vertikal dalam histogram ridgeline ini selalu muncul pada nilai x yangsama persis, bar dari histogram yang berbeda selaras satu sama lain dengan cara yang membingungkan. Menurut pendapat saya, lebih baik tidak menggambar histogram yang tumpang tindih.

Gambar 9.10: Suhu di Lincoln, Nebraska, pada 2016, divisualisasikan sebagai plot ridgeline histogram. Masing-masing histogram tidak terpisah dengan baik secara visual, dan gambaran keseluruhannya cukup sibuk dan membingungkan.
Skala plot Ridgeline ke jumlah distribusi yang sangat besar.Sebagai contoh, Gambar 9.11 menunjukkan distribusi panjang film dari tahun 1913 hingga 2005. Angka ini berisi hampir 100 distribusi yang berbeda namun sangat mudah dibaca. Kita dapat melihat bahwa pada 1920-an, film datang dalam banyak panjang yang berbeda, tetapi sejak sekitar 1960 panjang film telah distandarisasi menjadi sekitar 90 menit.

Gambar 9.11: Evolusi panjang film seiring waktu. Sejak 1960-an, mayoritas semua film berdurasi sekitar 90 menit. Sumber data: Internet Movie Database, IMDB
Plot Ridgeline juga berfungsi dengan baik jika kita ingin membandingkan dua tren dari waktu ke waktu. Ini adalah skenario yang muncul secara umum jika kita ingin menganalisis pola pemungutan suara anggota dari dua partai yang berbeda. Kita dapat membuat perbandingan ini dengan mengejutkan distribusi secara vertikal berdasarkan waktu dan menggambar dua distribusi warna berbeda pada setiap titik waktu, mewakili kedua pihak (Gambar 9.12 ).

Gambar 9.12: Pola pemilihan di DPR AS menjadi semakin terpolarisasi.Skor DW-NOMINASI sering digunakan untuk membandingkan pola pemilihan perwakilan antar partai dan dari waktu ke waktu. Di sini, distribusi skor ditunjukkan untuk setiap Kongres dari tahun 1963 hingga 2013 secara terpisah untuk Demokrat dan Republik. Setiap Kongres diwakili oleh tahun pertamanya. Konsep tokoh asli: McDonald ( 2017 ) .
Referensi
Sidiropoulos, N., SH Sohi, TL Pedersen, BT Porse, O. Winther, N. Rapin, dan FO Bagger. 2018. “SinaPlot: Bagan yang Ditingkatkan untuk Representasi Sederhana dan Jujur dari Pengamatan Tunggal atas Berbagai Kelas.” J. Comp.Grafik. Stat 27: 673-76. doi: 10.1080 / 10618600.2017.1366914 .
Wehrwein, Austin. 2017. "Ini Membawa Saya Ggjoy."http://austinwehrwein.com/data-visualization/it-brings-me-ggjoy/ .
McDonald, Ian. 2017. "DW-NOMINASI Menggunakan Ggjoy."http://rpubs.com/ianrmcdonald/293304 .




