Bab 3 Pemodelan Data R
3.1 Bayangkan Ini
Tim proyek Anda ditugaskan untuk bekerja dengan tim piutang. Khususnya, piutang akan meninjau portofolio pelanggan dari potensi akuisisi. Manajer ingin meminta data yang diberikan melalui uji tuntas selama proses akuisisi.Beberapa pertanyaan meliputi:
- Apa risiko pendapatan di seluruh pelamar?
- Apakah ada perbedaan dalam pendapatan pemohon?
- Apakah usia itu penting?
- Apakah ada pola tanggungan keluarga di seluruh kelompok pemohon?
- Berapa penghasilan per tanggungan?
Tim analisis akan memproses data, meninjau kualitasnya, dan membantu akun yang dapat diterima menjawab pertanyaan-pertanyaan ini.
Dalam bab ini kami akan membangun pendekatan untuk mengelola kueri tersebut, termasuk tabel pivot, pencarian, dan pembuatan metrik baru dari data yang ada. Kami akan memperluas berbagai keterampilan ini ke dalam penulisan fungsi, seperti net present value dan internal rate of return, lebih banyak memplot data, bekerja dengan data deret waktu, dan menyesuaikan data dengan distribusi probabilitas.
3.2 tabel Pivot dan Pencarian Vertikal
Ini, setidaknya secara mitos, adalah dua dari fitur Excel yang paling banyak digunakan. Tabel pivot adalah mesin irisan dan dadu yang kami gunakan untuk mempartisi set data.Pencarian memungkinkan kami untuk menghubungkan satu tabel data ke yang lain. Kami akan menjelajahi alat-alat ini di
R , di sini menjadi lebih mudah dan kurang tepat untuk crash pada set data yang besar. Kami mulai dengan beberapa definisi.3.2.1 Beberapa definisi
Tabel pivot adalah alat perangkuman data yang dapat secara otomatis mengurutkan, menghitung, total, atau memberikan rata-rata data yang disimpan dalam satu tabel atau spreadsheet, menampilkan hasilnya dalam tabel kedua yang menunjukkan data yang dirangkum. Alat ini mengubah tabel bidang datar dengan baris data menjadi tabel dengan nilai baris yang dikelompokkan dan nilai header kolom. Spesifikasi nilai baris yang dikelompokkan dan header kolom dapat memutar data baris tabel datar ke persimpangan baris dan label kolom.
"V" atau "vertikal" adalah singkatan dari mencari nilai dalam sebuah kolom. Fitur ini memungkinkan analis untuk menemukan kecocokan perkiraan dan tepat antara nilai pencarian dan nilai tabel dalam kolom vertikal yang ditetapkan untuk nilai pencarian. Fungsi
HLOOKUP melakukan pencarian yang sama tetapi untuk baris yang ditentukan, bukan kolom.3.2.2 Pivot dan Parry
Mari kita kembali ke pertanyaan bisnis Pemohon Kartu Kredit:
- Apa risiko pendapatan di seluruh pelamar?
- Apakah ada perbedaan dalam pendapatan pemohon?
- Apakah usia itu penting?
- Apakah ada pola tanggungan antar kelompok pemohon?
- Berapa penghasilan per tanggungan?
Langkah pertama dalam membangun analisis data relatif terhadap pertanyaan-pertanyaan ini adalah untuk memahami dimensi data yang diperlukan yang berlaku untuk pertanyaan. Di sini kita akan memindai nama kolom tabel dalam basis data dan mencari
- Status kartu
- Kepemilikan
- Pekerjaan
CreditCard <- read.csv ( "data/CreditCard.csv" ) str (CreditCard) ## 'data.frame': 1319 obs. of 13 variables: ## $ card : Factor w/ 2 levels "no","yes": 2 2 2 2 2 2 2 2 2 2 ... ## $ reports : int 0 0 0 0 0 0 0 0 0 0 ... ## $ age : num 37.7 33.2 33.7 30.5 32.2 ... ## $ income : num 4.52 2.42 4.5 2.54 9.79 ... ## $ share : num 0.03327 0.00522 0.00416 0.06521 0.06705 ... ## $ expenditure: num 124.98 9.85 15 137.87 546.5 ... ## $ owner : Factor w/ 2 levels "no","yes": 2 1 2 1 2 1 1 2 2 1 ... ## $ selfemp : Factor w/ 2 levels "no","yes": 1 1 1 1 1 1 1 1 1 1 ... ## $ dependents : int 3 3 4 0 2 0 2 0 0 0 ... ## $ months : int 54 34 58 25 64 54 7 77 97 65 ... ## $ majorcards : int 1 1 1 1 1 1 1 1 1 1 ... ## $ active : int 12 13 5 7 5 1 5 3 6 18 ... ## $ state : Factor w/ 3 levels "CT","NJ","NY": 3 3 3 3 3 3 3 3 3 3 ... Fungsi
str() memungkinkan kita untuk melihat semua objek di CreditCard . Berikutnya, lihat data itu sendiri di dalam objek ini menggunakan head (untuk awal data). head (CreditCard, 3 ) ## card reports age income share expenditure owner selfemp ## 1 yes 0 37.66667 4.52 0.033269910 124.983300 yes no ## 2 yes 0 33.25000 2.42 0.005216942 9.854167 no no ## 3 yes 0 33.66667 4.50 0.004155556 15.000000 yes no ## dependents months majorcards active state ## 1 3 54 1 12 NY ## 2 3 34 1 13 NY ## 3 4 58 1 5 NY Mengetahui struktur dan sampel data, kita dapat membangun ringkasan data dan meninjau minimum, maksimum, dan kuartil di setiap kolom data
CreditCard . summary (CreditCard) ## card reports age income ## no : 296 Min. : 0.0000 Min. : 0.1667 Min. : 0.210 ## yes:1023 1st Qu.: 0.0000 1st Qu.:25.4167 1st Qu.: 2.244 ## Median : 0.0000 Median :31.2500 Median : 2.900 ## Mean : 0.4564 Mean :33.2131 Mean : 3.365 ## 3rd Qu.: 0.0000 3rd Qu.:39.4167 3rd Qu.: 4.000 ## Max. :14.0000 Max. :83.5000 Max. :13.500 ## share expenditure owner selfemp ## Min. :0.0001091 Min. : 0.000 no :738 no :1228 ## 1st Qu.:0.0023159 1st Qu.: 4.583 yes:581 yes: 91 ## Median :0.0388272 Median : 101.298 ## Mean :0.0687322 Mean : 185.057 ## 3rd Qu.:0.0936168 3rd Qu.: 249.036 ## Max. :0.9063205 Max. :3099.505 ## dependents months majorcards active ## Min. :0.0000 Min. : 0.00 Min. :0.0000 Min. : 0.000 ## 1st Qu.:0.0000 1st Qu.: 12.00 1st Qu.:1.0000 1st Qu.: 2.000 ## Median :1.0000 Median : 30.00 Median :1.0000 Median : 6.000 ## Mean :0.9939 Mean : 55.27 Mean :0.8173 Mean : 6.997 ## 3rd Qu.:2.0000 3rd Qu.: 72.00 3rd Qu.:1.0000 3rd Qu.:11.000 ## Max. :6.0000 Max. :540.00 Max. :1.0000 Max. :46.000 ## state ## CT:442 ## NJ:472 ## NY:405 ## ## ## Kami segera melihat usia minimum 0,2. Entah ini anomali, atau kesalahan total, atau ada aplikasi yang belum berumur setahun !. Mari saring data untuk usia lebih dari 18 agar aman.
ccard <- CreditCard[CreditCard $ age >= 18 , ] Dalam filter, koma berarti menyimpan data pada pelamar hanya pada atau lebih dari 18 tahun. Ketika kami membiarkan kolom kosong, itu berarti menerapkan filter ini di semua kolom. Kami selanjutnya meninjau distribusi usia pelamar untuk memastikan filter kami melakukan pekerjaan dengan baik. Function
hist() membuat histogram frekuensi sederhana untuk memvisualisasikan data ini. hist (ccard $ age) 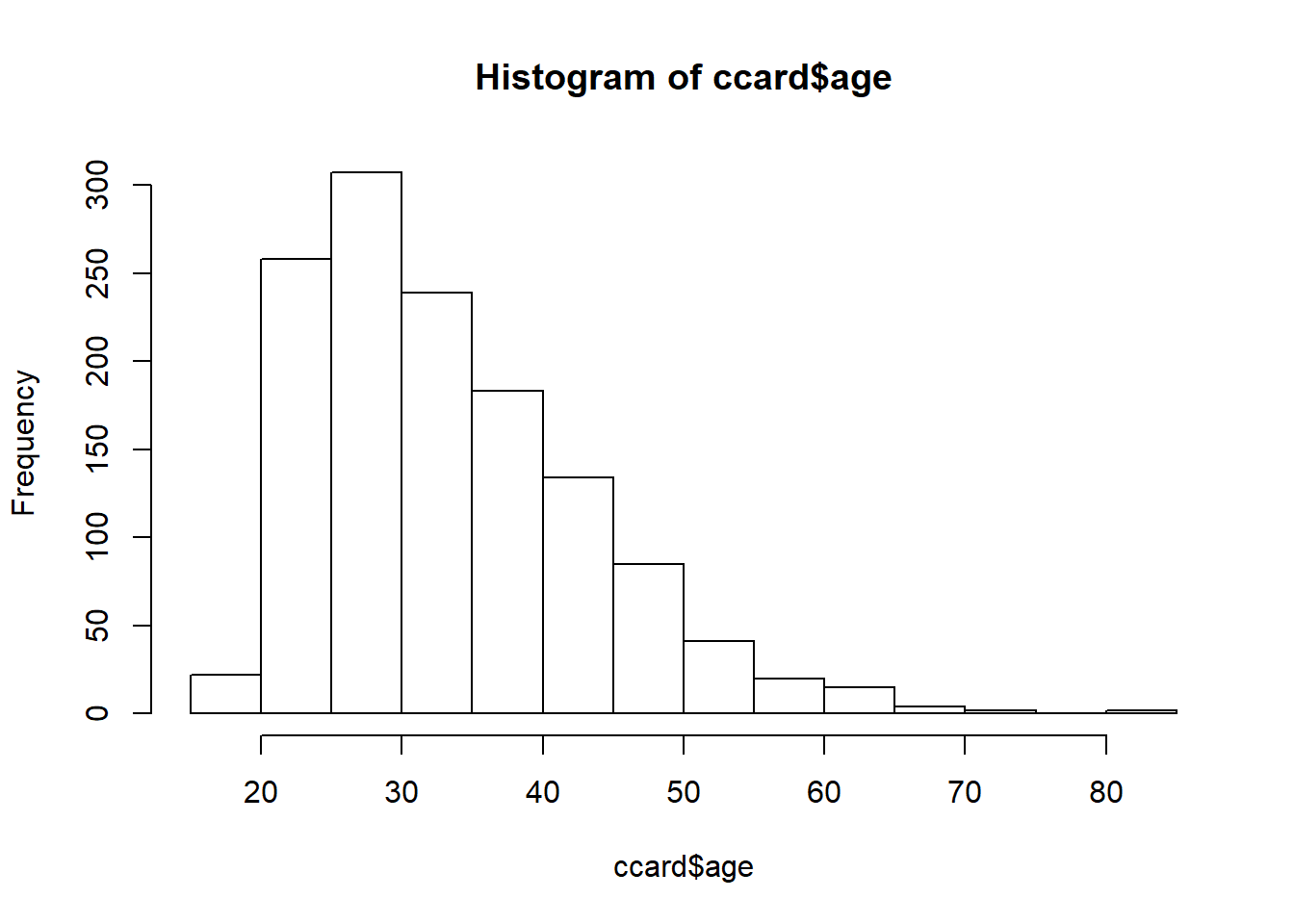
3.2.3 Coba latihan ini
Apa desain dasar dari pertanyaan ini?
- Pertanyaan bisnis?
- Ukuran?
- Taksonomi dan metrik?
Untuk menjawab 1 dan 2 kami memiliki pertanyaan bisnis di sepanjang garis variabel indikator:
- Kartu yang dikeluarkan (
card) - Memiliki atau menyewakan (
owner) - Wiraswasta atau tidak (
selfemp)
Untuk 3 taksonomi dasar kita adalah:
- Untuk setiap kartu yang dikeluarkan ... di New York
- ... dan untuk setiap pemilik ...
- ... siapa yang dipekerjakan ...
- Berapa kisaran pendapatan, tanggungan rata-rata, usia, dan pendapatan per tanggungan?
Berikut adalah desain tabel 3 langkah dasar pivot. Kita harus memeriksa apakah kita telah menginstal paket
dplyr ke lingkungan R # install.packages('dplyr') if not # already require (dplyr) ## 1: filter to keep three states. pivot.table <- filter (ccard, state %in% "NY" ) ## 2: set up data frame for by-group ## processing. pivot.table <- group_by (pivot.table, card, owner, selfemp) ## 3: calculate the three summary ## metrics options ( dplyr.width = Inf ) ## to display all columns pivot.table <- summarise (pivot.table, income.cv = sd (income) / mean (income), age.avg = mean (age), income.per.dependent = sum (income) / sum (dependents)) Kami kemudian memvisualisasikan hasil dalam tabel. Di sini kita menggunakan
knitr , yang merupakan paket yang rmarkdown . Function kable() adalah kependekan dari “table knitr.” knitr :: kable (pivot.table) | kartu | pemilik | selfemp | income.cv | age.avg | income.per.dependent |
|---|---|---|---|---|---|
| tidak | tidak | tidak | 0.4941859 | 31.91936 | 3.645848 |
| tidak | tidak | Iya | 0,5652634 | 26.38542 | 2.852000 |
| tidak | Iya | tidak | 0,3756274 | 36.01786 | 2.157589 |
| tidak | Iya | Iya | NaN | 53.33333 | Inf |
| Iya | tidak | tidak | 0,3298633 | 28.09311 | 5.313677 |
| Iya | tidak | Iya | 0,4367858 | 37.45238 | 7.062500 |
| Iya | Iya | tidak | 0,5519888 | 36.79503 | 3.154476 |
| Iya | Iya | Iya | 0,5032180 | 41.91667 | 3.194547 |
3.2.4 Sekarang ke VLOOKUP
Mari kita mulai dengan kumpulan data yang berbeda. Kami memuat data IBRD (Bank Dunia) ini
- Variabel
life.expectancyadalah harapan hidup rata-rata untuk setiap negara dari 2009 hingga 2014. sanitationvariabel adalah persentase populasi dengan akses langsung ke fasilitas sanitasi.
le <- read.csv ( "data/life_expectancy.csv" , header = TRUE , stringsAsFactors = FALSE ) sa <- read.csv ( "data/sanitation_.csv" , header = TRUE , stringsAsFactors = FALSE ) Kami selalu melihat beberapa catatan pertama.
head (le) ## country years.life.expectancy.avg ## 1 Afghanistan 46.62135 ## 2 Albania 71.11807 ## 3 Algeria 61.81652 ## 4 Angola 41.65847 ## 5 Antigua and Barbuda 69.81219 ## 6 Arab World 60.93432 head (sa) ## country sanitation.avg ## 1 Afghanistan 25.39600 ## 2 Albania 85.36154 ## 3 Algeria 84.21538 ## 4 American Samoa 61.73077 ## 5 Andorra 100.00000 ## 6 Angola 36.00769 Pekerjaan di sini adalah untuk menggabungkan data sanitasi dengan data harapan hidup, berdasarkan negara. Dalam Excel kami biasanya menggunakan pernyataan
VLOOKUP(country, sanitation, 2, FALSE) .- Dalam pernyataan ini
countryadalah nilai yang harus dilihat, misalnya, "Australia". sanitationvariabel adalah kisaran tabel pencarian sanitasi dua kolom data negara dan sanitasi, misalnya,B2:C104di Excel.- Angka
2adalah kolom kedua dari tabel pencarian sanitasi, misalnya kolomC FALSEberarti tidak menemukan yang sama persis.
Di
R kita bisa menggunakan fungsi merge() . life.sanitation <- merge (le[, c ( "country" , "years.life.expectancy.avg" )], sa[, c ( "country" , "sanitation.avg" )]) Seluruh jajaran negara dihuni oleh pencarian.
head (life.sanitation, 3 ) ## country years.life.expectancy.avg sanitation.avg ## 1 Afghanistan 46.62135 25.39600 ## 2 Albania 71.11807 85.36154 ## 3 Algeria 61.81652 84.21538 3.2.5 Coba latihan ini
Kami akan memuat data lain yang ditetapkan pada harga rumah. Misalkan kita bekerja untuk pengembang perumahan seperti Toll Brothers (NYSE: TOL) dan ingin mengalokasikan sumber daya untuk memasarkan dan membiayai pembangunan rumah mewah di wilayah metropolitan utama AS. Kami memiliki data untuk satu pasar pengujian.
hprice <- read.csv ( "data/hprice.csv" ) Mari kita lihat data yang tersedia:
summary (hprice) ## ID Price SqFt Bedrooms ## Min. : 1.00 Min. : 69100 Min. :1450 Min. :2.000 ## 1st Qu.: 32.75 1st Qu.:111325 1st Qu.:1880 1st Qu.:3.000 ## Median : 64.50 Median :125950 Median :2000 Median :3.000 ## Mean : 64.50 Mean :130427 Mean :2001 Mean :3.023 ## 3rd Qu.: 96.25 3rd Qu.:148250 3rd Qu.:2140 3rd Qu.:3.000 ## Max. :128.00 Max. :211200 Max. :2590 Max. :5.000 ## Bathrooms Offers Brick Neighborhood ## Min. :2.000 Min. :1.000 No :86 East :45 ## 1st Qu.:2.000 1st Qu.:2.000 Yes:42 North:44 ## Median :2.000 Median :3.000 West :39 ## Mean :2.445 Mean :2.578 ## 3rd Qu.:3.000 3rd Qu.:3.000 ## Max. :4.000 Max. :6.000 Pertanyaan bisnis kami meliputi:
- Lingkungan apa yang paling berharga (harga lebih tinggi)?
- Karakteristik perumahan apa yang paling mempertahankan nilai perumahan?
Pertama, di mana dan apa rumah paling berharga? Salah satu cara untuk menjawab ini adalah dengan membangun tabel pivot. Selanjutnya kita pivot data dan membangun metrik ke dalam kueri. Kami akan menggunakan fungsi
mean() dan standar deviasi sd() untuk membantu menjawab pertanyaan kami. require (dplyr) ## 1: filter to those houses with ## fairly high prices pivot.table <- filter (hprice, Price > 99999 ) ## 2: set up data frame for by-group ## processing pivot.table <- group_by (pivot.table, Brick, Neighborhood) ## 3: calculate the summary metrics options ( dplyr.width = Inf ) ## to display all columns pivot.table <- summarise (pivot.table, Price.avg = mean (Price), Price.cv = sd (Price) / mean (Price), SqFt.avg = mean (SqFt), Price.per.SqFt = mean (Price) / mean (SqFt)) Lalu kami memvisualisasikannya dalam sebuah tabel.
knitr :: kable (pivot.table) | Bata | Lingkungan | Harga | Harga.cv | SqFt.avg | Harga.per.qqt |
|---|---|---|---|---|---|
| Tidak | Timur | 121095.7 | 0,1251510 | 2019.565 | 59.96125 |
| Tidak | Utara | 115307.1 | 0,0939797 | 1958.214 | 58.88382 |
| Tidak | Barat | 148230.4 | 0,0912350 | 2073.478 | 71.48878 |
| Iya | Timur | 135468.4 | 0,0977973 | 2031.053 | 66.69863 |
| Iya | Utara | 118457.1 | 0,1308498 | 1857.143 | 63.78462 |
| Iya | Barat | 175200.0 | 0,0930105 | 2091.250 | 83.77764 |
Berdasarkan kumpulan data ini dari satu wilayah metropolitan, properti paling berharga (mengambil harga rata-rata tertinggi dan harga per kaki persegi) terbuat dari batu bata di lingkungan Barat. Brick atau tidak, lingkungan Barat juga tampaknya memiliki variasi harga relatif terendah.
Sekarang untuk sesuatu yang berbeda: fungsi.
3.3 Mengapa Berfungsi?
Kami akan merangkum beberapa operasi ke dalam perangkat penyimpanan yang dapat digunakan kembali yang disebut fungsi. Tersangka dan kandidat yang biasa untuk penggunaan fungsi adalah:
- Struktur data menyatukan nilai-nilai terkait menjadi satu objek.
- Fungsi grup terkait perintah menjadi satu objek.
Dalam kedua kasus itu, logika dan pengkodean lebih mudah dipahami, lebih mudah dikerjakan, lebih mudah dibangun menjadi hal-hal yang lebih besar, dan lebih tidak rentan terhadap pelanggaran-pelanggaran jari yang sederhana dan tua tentang keselamatan dan keamanan operasional.
Misalnya, di sini adalah fungsi NPV yang mirip Excel. Kami memasukkan ini ke dalam kode-potongan dalam file
R markdown atau langsung ke konsol untuk menyimpan fungsi ke lingkungan R saat ini. Setelah selesai, kita sekarang memiliki fungsi baru yang dapat kita gunakan seperti fungsi lainnya. ## Net Present Value function Inputs: ## vector of rates (rates) with 0 as ## the first rate for time 0, vector ## of cash flows (cashflows) Outputs: ## scalar net present value NPV. 1 <- function (rates, cashflows) { NPV <- sum (cashflows / ( 1 + rates) ^ ( seq_along (cashflows) - 1 )) return (NPV) } Struktur fungsi memiliki bagian-bagian ini:
- Header menjelaskan fungsi beserta input dan outputnya.Di sini kita menggunakan karakter komentar
#untuk menggambarkan dan mendokumentasikan fungsi. - Definisi memberi nama fungsi dan mengidentifikasi antarmuka input dan output ke lingkungan pemrograman. Namanya seperti variabel dan ditugaskan ke
function(), di mana input didefinisikan. - Pernyataan kode mengambil input dari definisi dan memprogram tugas, logika, dan keputusan dalam alur kerja fungsi menjadi output.
- Pernyataan keluaran merilis hasil fungsi untuk digunakan dalam pernyataan kode lain di luar "ayat mini" fungsi.Kami menggunakan fungsi formal
return()untuk mengidentifikasi output yang akan dihasilkan oleh fungsi tersebut. Jika kita tidak menggunakanreturn(), makaRakan memberikan kita variabel yang ditugaskan terakhir sebagai output dari fungsi.
Dalam contoh ini, kami menghasilkan data internal ke fungsi:
- Kami menggunakan
seq_alonguntuk menghasilkan indeks waktu arus kas. - Kita harus mengurangi 1 dari urutan ini karena memulai arus kas adalah waktu 0.
- Kami menghasilkan nilai sekarang bersih secara langsung dalam satu baris kode.
Fungsi kami digunakan seperti yang ada di dalamnya, misalnya
mean() . Mari kita tetapkan rates dan cashflowssebagai input vektor ke fungsi NPV.1() dan jalankan kode ini. rates <- c ( 0 , 0.08 , 0.06 , 0.04 ) ## first rate is always 0.00 cashflows <- c ( - 100 , 200 , 300 , 10 ) NPV.1 (rates, cashflows) ## [1] 361.0741 Kami kembali ke deklarasi dan melihat bagian-bagiannya:
## Net Present Value function Inputs: ## vector of rates (rates) with 0 as ## the first rate for time 0, vector ## of cash flows (cashflows) Outputs: ## scalar net present value NPV. 1 <- function (rates, cashflows) { NPV <- sum (cashflows / ( 1 + rates) ^ ( seq_along (cashflows) - 1 )) return (NPV) } Antarmuka merujuk pada komponen ini:
- input atau argumen
- output atau nilai pengembalian
- Memanggil fungsi-fungsi lain,
seq_along(), operator/,+,^dan-.
Kami juga dapat memanggil fungsi lain yang telah kami tulis.Kami menggunakan
return() untuk secara eksplisit mengatakan apa outputnya. Ini hanya dokumentasi yang bagus. Bergantian, fungsi akan mengembalikan evaluasi terakhir.Komentar, yaitu, baris yang dimulai dengan
# , tidak diperlukan oleh R , tetapi selalu merupakan ide yang baik dan disambut yang memberikan deskripsi singkat tentang tujuan dan arah. Komentar awal juga harus mencakup daftar input, juga disebut "argumen," dan output.3.3.1 Apa yang seharusnya menjadi fungsi?
Fungsi harus ditulis untuk kode yang akan kita jalankan kembali, terutama jika akan dijalankan kembali dengan perubahan input. Mereka juga bisa menjadi potongan kode yang terus kami sorot dan tekan return on. Kita sering menulis fungsi untuk chunk kode yang merupakan bagian kecil dari analisis yang lebih besar.
Dalam edisi berikutnya dari
irr.1 kami meningkatkan kode dengan argumen nama dan default. ## Internal Rate of Return (IRR) ## function Inputs: vector of cash ## flows (cashflows), scalar ## interations (maxiter) Outputs: ## scalar net present value IRR. 1 <- function (cashflows, maxiter = 1000 ) { t <- seq_along (cashflows) - 1 ## rate will eventually converge to ## IRR f <- function (rate) ( sum (cashflows / ( 1 + rate) ^ t)) ## use uniroot function to solve for ## root (IRR = rate) of f = 0 c(-1,1) ## bounds solution for only positive ## or negative rates select the root ## estimate return ( uniroot (f, c ( - 1 , 1 ), maxiter = maxiter) $ root) } Di sini argumen default adalah
maxiter yang mengontrol jumlah iterasi. Pada risiko kita, kita dapat menghilangkan argumen ini jika kita mau. Ini menggambarkan kebutuhan lain akan fungsi: kita dapat menempatkan logika kesalahan dan pengecualian untuk menangani beberapa masalah fatal yang mungkin muncul dalam perhitungan kita.Berikut adalah arus kas untuk obligasi kupon 3% yang dibeli dengan premi yang lumayan.
cashflows <- c ( - 150 , 3 , 3 , 3 , 3 , 3 , 3 , 3 , 103 ) IRR.1 (cashflows) ## [1] -0.02554088 IRR.1 (cashflows, maxiter = 100 ) ## [1] -0.02554088 Kami mendapatkan IRR negatif atau hasil hingga jatuh tempo pada perhitungan net present value = 0 ini.
3.3.2 Masalah pengambilan gambar
Masalah : Kita melihat perilaku "aneh" ketika argumen tidak seperti yang kita harapkan.
NPV.1 ( c ( 0.1 , 0.05 ), c ( - 10 , 5 , 6 , 100 )) ## [1] 86.10434 Kami memang mendapatkan hasil, tapi ...
- Apa artinya?
- Tarif apa yang sesuai dengan arus kas apa?
Di sini fungsi menghitung nilai sekarang bersih. Tetapi analis memasukkan dua tingkat untuk empat arus kas.
Solusi : Kami memasukkan cek kewarasan ke dalam kode.
- Mari kita gunakan
stopifnot(some logical statment)yang BENAR.
## Net Present Value function Inputs: ## vector of rates (rates) with 0 as ## the first rate for time 0, vector ## of cash flows (cashflows), length ## of rates must equal length of ## cashflows Outputs: scalar net ## present value NPV. 2 <- function (rates, cashflows) { stopifnot ( length (rates) == length (cashflows)) NPV <- sum (cashflows / ( 1 + rates) ^ ( seq_along (cashflows) - 1 )) return (NPV) } Berikut adalah beberapa pemikiran tentang
stopifnot TRUEpenanganan kesalahan- Argumen untuk
stopifnot()adalah serangkaian ekspresi logis yang semuanya harus BENAR. - Eksekusi terhenti, dengan pesan kesalahan, pada awalnya SALAH.
NPV.2 ( c ( 0.1 , 0.05 ), c ( - 10 , 5 , 6 , 100 )) Tekan (tidak terlalu keras!) Tombol
Escape di keyboard Anda, Ini akan membawa Anda keluar dari mode Browse[1]> dan kembali ke prompt konsol > .3.3.3 Apa yang dapat dilihat dan dilakukan fungsi
Setiap fungsi memiliki lingkungannya sendiri. Nama-nama di sini akan menggantikan nama di lingkungan global.Lingkungan internal fungsi dimulai dengan argumen yang dinamai. Tugas di dalam fungsi hanya mengubah lingkungan internal. Jika nama tidak didefinisikan dalam fungsi, fungsi akan mencari nama ini di lingkungan tempat fungsi dipanggil.
3.3.4 Coba ini ...
Perusahaan Anda menjalankan proyek 100 juta pound sterling di UE. Anda harus memasukkan jaminan 25% di Landesbank hanya menggunakan sekuritas pemerintah berkualitas tinggi. Anda menemukan dana emas berkualitas tinggi yang akan membayar 1,5% (tingkat kupon) setiap tahun selama tiga tahun.
Beberapa pertanyaan untuk dianalisis
- Berapa yang akan Anda bayar untuk agunan ini jika kurva nilai (hasil hingga jatuh tempo arus kas) adalah (mulai tahun depan pada ...)
rates <- c ( - 0.001 , 0.002 , 0.01 ) - Misalkan dealer obligasi meminta 130% dari nilai jaminan nosional untuk obligasi ini. Berapa hasil dari transaksi ini (IRR)? Apakah Anda akan membelinya?
- Apa pengembalian dari jaminan ini jika Anda menghentikan proyek dalam satu tahun dan melikuidasi jaminan (yaitu, menjualnya dengan uang tunai) jika hasilnya bergeser turun 0,005? Ini adalah pergeseran "paralel", yang merupakan pembiayaan untuk: "ambil setiap kurs dan kurangi 0,005."
Untuk mendapatkan persyaratan ini, kami akan membangun tarif dan arus kas di seluruh kerangka waktu 3 tahun, mengingat pekerjaan kami sebelumnya.
(rates <- c ( 0 , rates)) ## [1] 0.000 -0.001 0.002 0.010 collateral.periods <- 3 collateral.rate <- 0.25 collateral.notional <- collateral.rate * 100 coupon.rate <- 0.015 cashflows <- rep (coupon.rate * collateral.notional, collateral.periods) cashflows[collateral.periods] <- collateral.notional + cashflows[collateral.periods] (cashflows <- c ( 0 , cashflows)) ## [1] 0.000 0.375 0.375 25.375 Apa yang baru saja terjadi?
- Kami menambahkan
0ke jadwal tingkat sehingga kami dapat menggunakan fungsiNPV.2. - Kami kemudian membuat parameter term sheet (ketentuan transaksi jaminan),
- Kami menggunakan
rep()untuk membentuk arus kas kupon. - Kemudian kami menambahkan pembayaran nilai nosional ke arus kas terakhir.
Sekarang kita dapat menghitung nilai sekarang dari ikatan menggunakan
NPV.2 . (Value. 0 <- NPV.2 (rates, cashflows)) ## [1] 25.3776 Jawabannya adalah 25,378 juta pound sterling atau
Value.0 / collateral.notional kali nilai nosional.Hasil hingga jatuh tempo rata-rata kurs forward di seluruh arus kas obligasi. “Forward rate” adalah kurs per periode yang kami harapkan untuk dapatkan setiap periode. Ini adalah salah satu interpretasi dari Tingkat Pengembalian Internal (“IRR”).
cashflows.IRR <- cashflows collateral.ask <- 130 cashflows.IRR[ 1 ] <- - (collateral.ask / 100 ) * collateral.notional ## mind the negative sign! (collateral.IRR. 1 <- IRR.1 (cashflows.IRR)) ## [1] -0.07112366 Anda akhirnya membayar lebih dari 7% per tahun untuk hak istimewa memiliki ikatan ini! Anda menelepon Bank Sentral Eropa, melaporkan potongan rambut yang terlalu besar pada proyek Anda. Anda mengirimkan permintaan untuk proposal ke dealer obligasi lainnya. Mereka kembali dengan harga permintaan rata-rata 109 (109% dari nosional).
cashflows.IRR <- cashflows collateral.ask <- 109 cashflows.IRR[ 1 ] <- - (collateral.ask / 100 ) * collateral.notional (collateral.IRR. 1 <- IRR.1 (cashflows.IRR)) ## [1] -0.01415712 Itu lebih seperti itu: sekitar 140 basis poin (1,41% x 100 basis poin per persentase) biaya (tanda negatif).
Mari kita bersantai proyek, dan transaksi jaminan, dalam 1 tahun. Misalkan kurva hasil dalam 1 tahun telah bergeser paralel dengan 0,005.
rate.shift <- - 0.005 rates. 1 <- c ( 0 , rates[ - 2 ]) + rate.shift cashflows. 1 <- c ( 0 , cashflows[ - 2 ]) (Value. 1 <- NPV.2 (rates. 1 , cashflows. 1 )) ## [1] 25.37541 (collateral.return. 1 <- Value. 1 / ( - cashflows.IRR[ 1 ]) - 1 ) ## [1] -0.0687923 Hasil ini jauh lebih banyak daripada pengembalian impas pada transaksi agunan:
(collateral.gainloss <- collateral.notional * collateral.return. 1 ) * 1e+06 ## [1] -1719807 ## adjust for millions of euros Itu mungkin gaji seseorang ... (dalam pound sterling).
3.3.5 Pikirkan Antarmuka!
Antarmuka menandai lingkungan bagian dalam yang terkendali untuk kode kami;
- Mereka memungkinkan kita untuk berinteraksi dengan seluruh sistem hanya di antarmuka.
- Argumen secara eksplisit memberi fungsi semua informasi yang dibutuhkan fungsi untuk beroperasi dan mengurangi risiko kebingungan dan kesalahan.
- Ada pengecualian seperti universal universal seperti \ (\ pi \) .
- Demikian juga, output hanya harus melalui nilai pengembalian.
Mari kita membangun distribusi (parametrik) selanjutnya.
3.4 Melakukan distribusi
Seperti biasa, mari kita memuat beberapa data, kali ini dari Biro Statistik Tenaga Kerja (BLS) dan memuat indeks harga ekspor-impor yang uraian dan grafiknya di http://data.bls.gov/timeseries/EIUIR?output_view=pct_1mth .Kami mencari simbol "EIUIR" dan "EIUIR100" dan mengunduh file teks yang kemudian kami konversi ke variabel yang dipisahkan koma atau file
csv di Excel. Kami menyimpan file csv di direktori dan membacanya ke dalam variabel yang disebut EIUIR . require (xts) require (zoo) EIUIR <- read.csv ( "data/EIUIR.csv" ) head (EIUIR) ## Date Value ## 1 2006-01-01 113.7 ## 2 2006-02-01 112.8 ## 3 2006-03-01 112.7 ## 4 2006-04-01 115.1 ## 5 2006-05-01 117.2 ## 6 2006-06-01 117.3 xmprice <- na.omit (EIUIR) ## to clean up any missing data str (xmprice) ## 'data.frame': 131 obs. of 2 variables: ## $ Date : Factor w/ 131 levels "2006-01-01","2006-02-01",..: 1 2 3 4 5 6 7 8 9 10 ... ## $ Value: num 114 113 113 115 117 ... Kita mungkin harus menginstal secara terpisah paket
xtsdan zoo yang menangani data deret waktu secara eksplisit.Fungsi str() menunjukkan bahwa kolom Value dalam bingkai data berisi seri harga ekspor. Kami kemudian menghitung logaritma natural dari harga dan menghitung perbedaan untuk mendapatkan tingkat pertumbuhan dari bulan ke bulan. Plot sederhana mengungkapkan aspek seri data untuk dijelajahi. xmprice.r <- as.zoo ( na.omit (( diff ( log (xmprice $ Value))))) ## compute rates head (xmprice.r) ## 1 2 3 4 5 ## -0.0079470617 -0.0008869180 0.0210718947 0.0180805614 0.0008528785 ## 6 ## 0.0076433493 plot (xmprice.r, type = "l" , col = "blue" , xlab = "Date" , main = "Monthly 2/2000-9/2016" ) 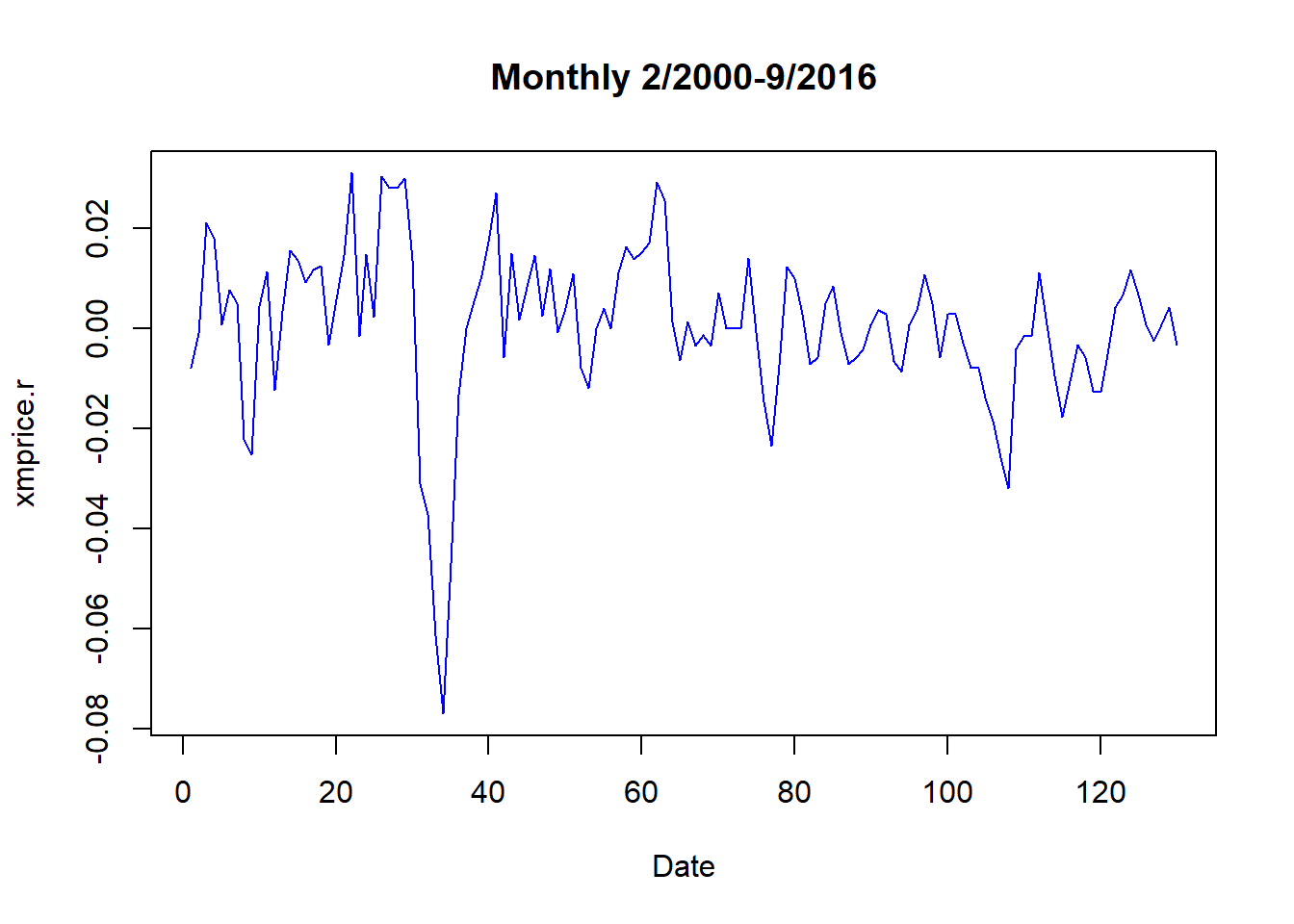
Kami selanjutnya mengubah data yang mengeksplorasi nilai absolut dari tingkat harga. Ini adalah langkah pertama untuk memahami pengelompokan volatilitas dalam deret waktu keuangan-ekonomi, suatu topik yang akan kita bahas kembali.
xmprice.r.df <- data.frame (xmprice.r, Date = index (xmprice.r), Rate = xmprice.r[, 1 ], Rate.abs <- abs (xmprice.r[, 1 ])) head (xmprice.r.df) ## xmprice.r Date Rate Rate.abs....abs.xmprice.r...1.. ## 1 -0.0079470617 1 -0.0079470617 0.0079470617 ## 2 -0.0008869180 2 -0.0008869180 0.0008869180 ## 3 0.0210718947 3 0.0210718947 0.0210718947 ## 4 0.0180805614 4 0.0180805614 0.0180805614 ## 5 0.0008528785 5 0.0008528785 0.0008528785 ## 6 0.0076433493 6 0.0076433493 0.0076433493 str (xmprice.r.df) ## 'data.frame': 130 obs. of 4 variables: ## $ xmprice.r : num -0.007947 -0.000887 0.021072 0.018081 0.000853 ... ## $ Date : int 1 2 3 4 5 6 7 8 9 10 ... ## $ Rate : num -0.007947 -0.000887 0.021072 0.018081 0.000853 ... ## $ Rate.abs....abs.xmprice.r...1..: num 0.007947 0.000887 0.021072 0.018081 0.000853 ... Kita dapat mencapai plot "lebih cantik" dengan paket
ggplot2 . Dalam pernyataan ggplot kami menggunakan aes , “estetika”, untuk memilih sumbu x (horizontal) dan y (vertikal). Menambahkan ( + ) geom_line adalah metode geometris yang membangun plot garis. require (ggplot2) ggplot (xmprice.r.df, aes ( x = Date, y = Rate)) + geom_line ( colour = "blue" ) 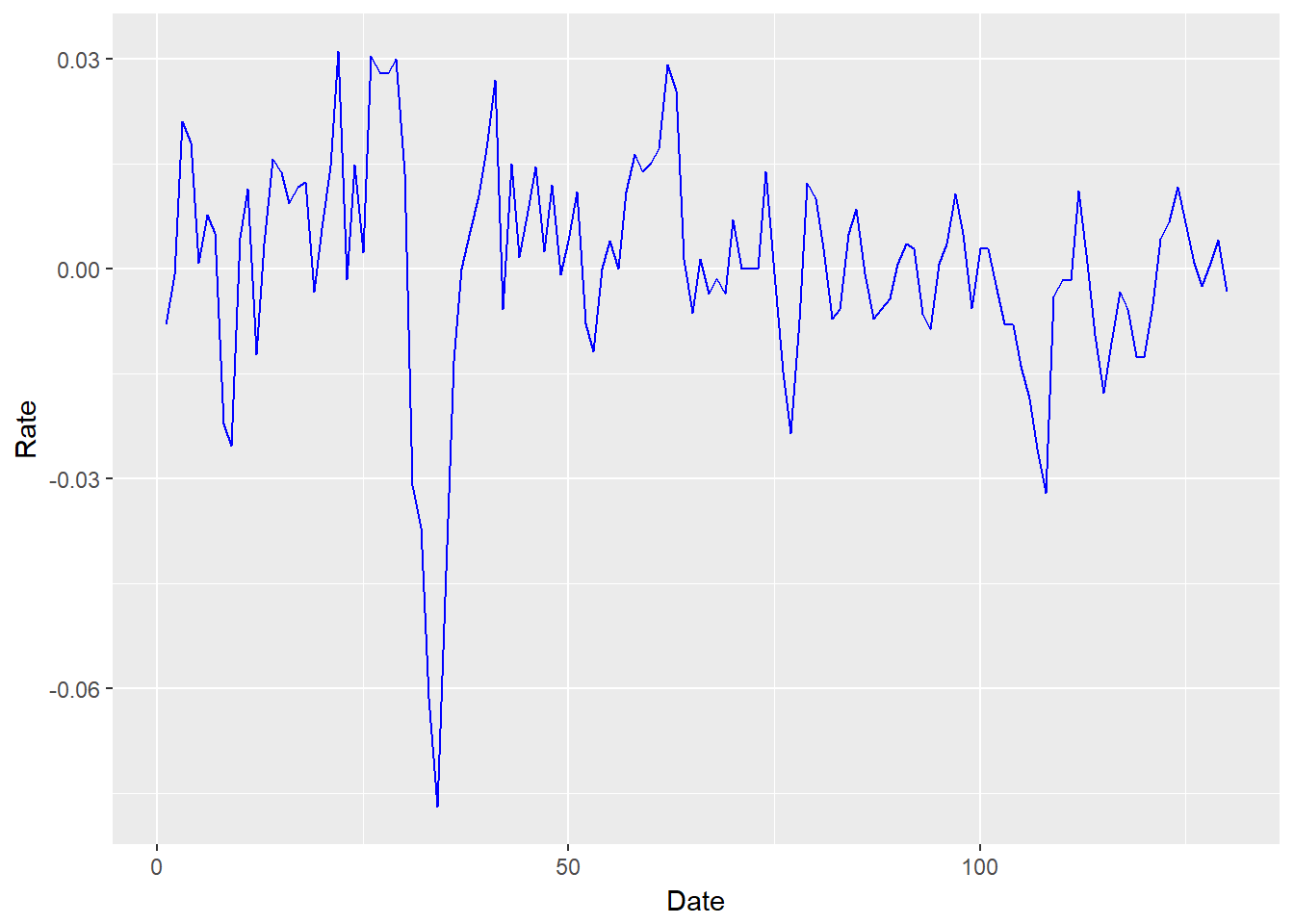
Mari kita coba grafik batang dari nilai absolut dari tingkat harga. Kami menggunakan
geom_bar untuk membuat gambar ini. require (ggplot2) ggplot (xmprice.r.df, aes ( x = Date, y = Rate.abs)) + geom_bar ( stat = "identity" , colour = "green" ) 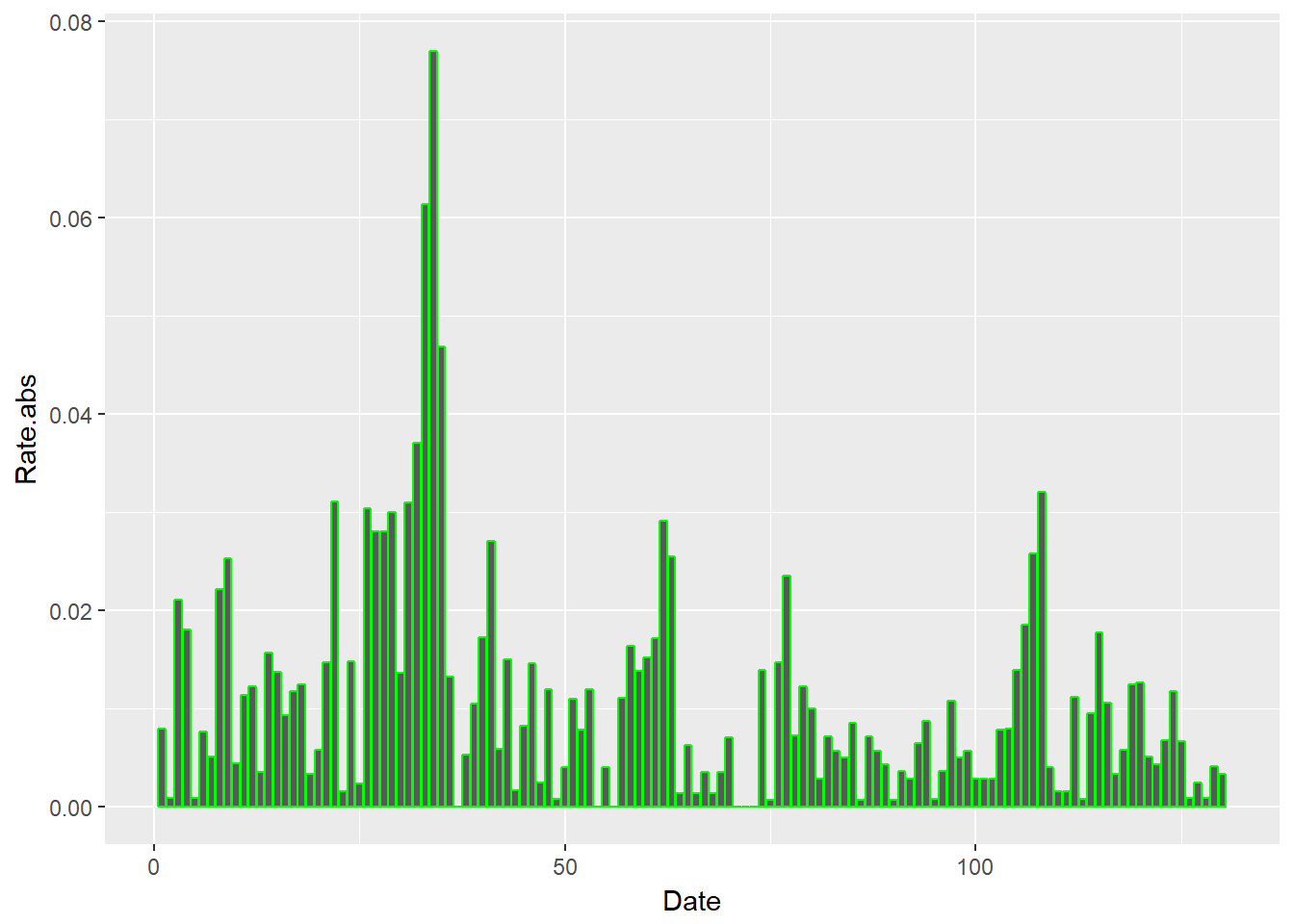
3.4.1 Cobalah latihan ini
Mari overlay kembali (
geom_line ) dan nilai geom_bar .ggplotmendeklarasikan kanvas menggunakan bingkai data harga.aesmenetapkan seri data yang akan digunakan untuk menghasilkan gambar.geom_barmembuat bagan batang.geom_linetumpanggeom_linebagan batang dengan bagan garis.
Dengan memeriksa bagan ini, pertanyaan bisnis apa tentang rantai pasokan Univeral Ekspor-Impor Ltd yang dapat membantu menjawab ini? Mengapa ini membantu?
require (ggplot2) ggplot (xmprice.r.df, aes (Date, Rate.abs)) + geom_bar ( stat = "identity" , colour = "darkorange" ) + geom_line ( data = xmprice.r.df, aes (Date, Rate), colour = "blue" ) 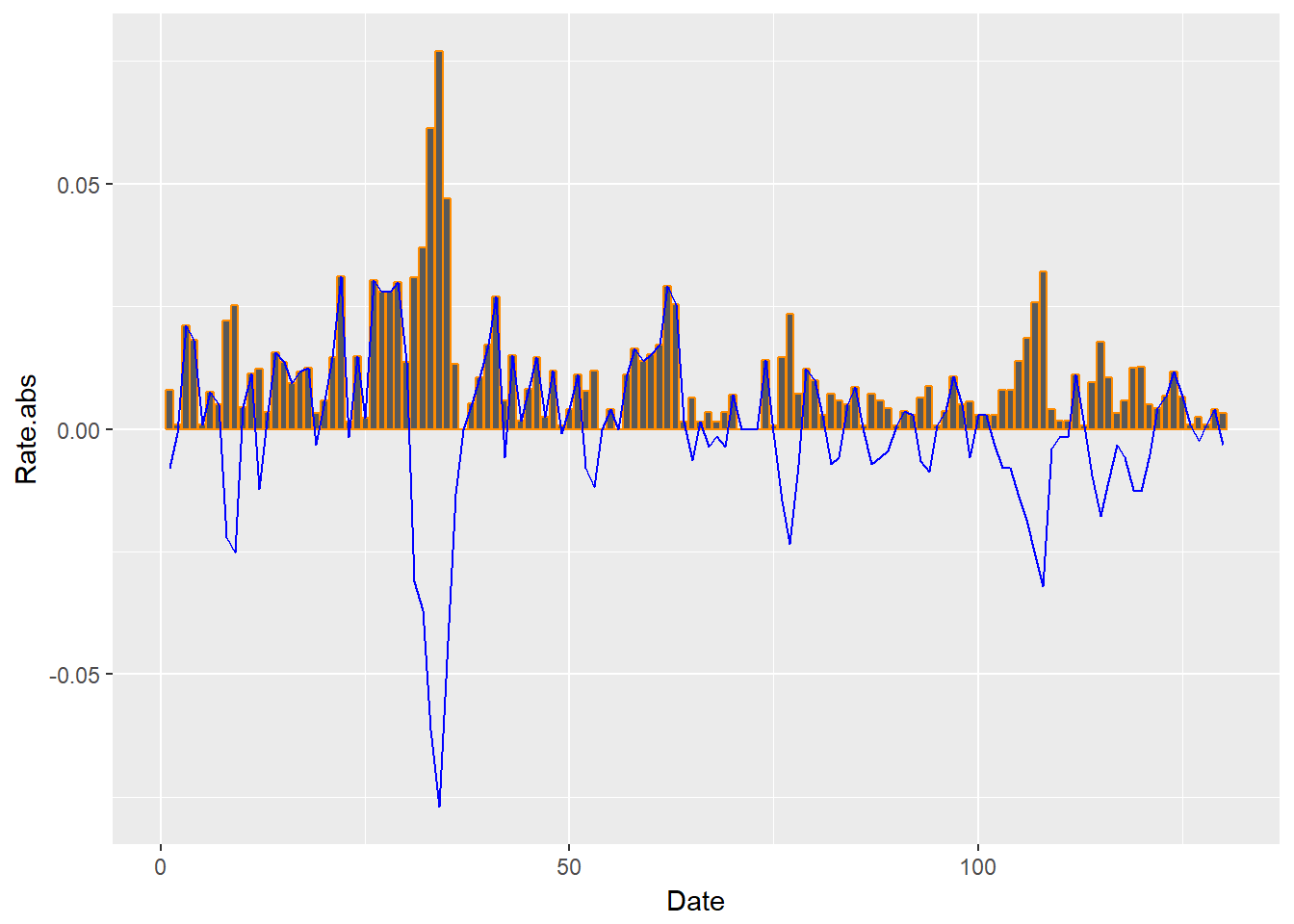
Plot berjalan jauh untuk menjawab pertanyaan: Ketika penawaran dan permintaan mengencang, apakah volatilitas harga mengelompok?
- Jika kita menjual, kita akan mengalami perubahan permintaan yang kuat dan dengan demikian dalam pendapatan di akhir pemenuhan pelanggan dari rantai.
- Jika kita membeli, kita akan mengalami ayunan kuat dalam biaya dan penggunaan input produk pada akhir pengadaan rantai.
- Untuk implikasi keuangan: kami akan mengalami kesulitan dalam menghasilkan pendapatan yang kami ramalkan ke pasar.
3.4.2 Bayangkan ini
Kami mengimpor barang sebagai input untuk proses manufaktur kami. Kami mungkin ingin mengetahui peluang bahwa tingkat ekspor-impor yang sangat tinggi mungkin terjadi. Kami dapat merencanakan panggilan fungsi distribusi kumulatif ( cdf atau CDF ). kita dapat membangun plot ini menggunakan fungsi
stat_ecdf() di ggplot2 . require (ggplot2) ggplot (xmprice.r.df, aes (Rate)) + stat_ecdf ( colour = "blue" ) 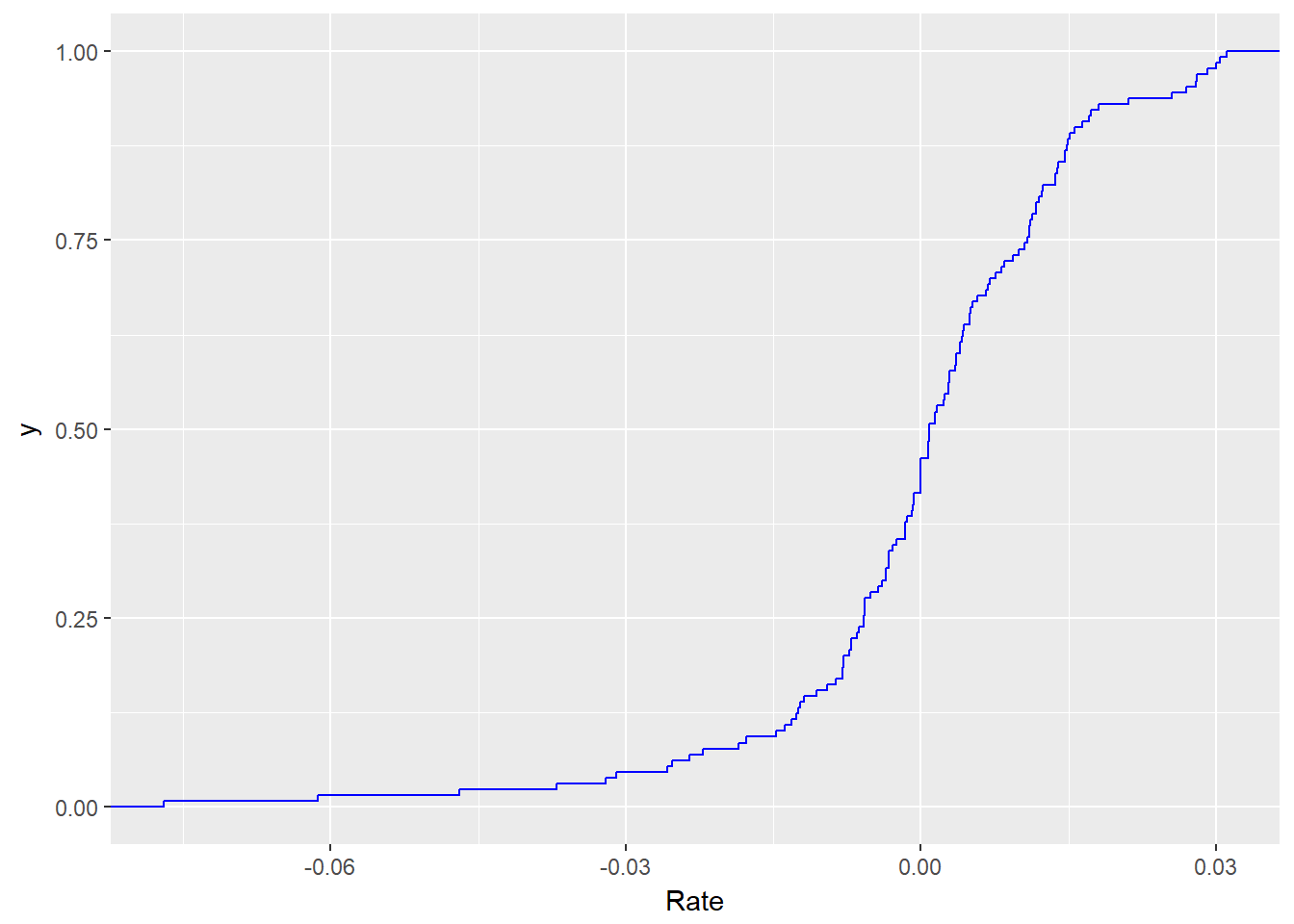
3.4.3 Coba latihan lain
- Misalkan delegasi dari otoritas yang berwenang mengirimkan pernyataan: “Pengadaan dapat menyetujui faktur input ketika hanya ada peluang 5% bahwa harga akan naik lebih tinggi daripada tingkat harga yang terkait dengan toleransi tersebut. Jika harga input benar-benar naik lebih tinggi dari tingkat yang dapat ditoleransi, Anda harus mendapatkan persetujuan divisi. "
- Plot garis vertikal untuk menunjukkan tingkat maksimum yang dapat ditoleransi untuk pengadaan menggunakan data BLS EIUR dari tahun 2000 hingga saat ini.
- Gunakan
r.tol <- quantile(xmprice.r.df$Rate, 0.95)untuk menemukan kurs yang dapat ditoleransi. - Gunakan
+ geom_vline(xintercept = r.tol)dalam plot CDF.
Kami dapat menerapkan persyaratan ini dengan kode berikut.
require (ggplot2) r.tol.pct <- 0.95 r.tol <- quantile (xmprice.r.df $ Rate, r.tol.pct) r.tol.label <- paste ( "Tolerable Rate = " , round (r.tol, 2 )) ggplot (xmprice.r.df, aes (Rate)) + stat_ecdf ( colour = "blue" , size = 1.5 ) + geom_vline ( xintercept = r.tol, colour = "red" , size = 1.5 ) + annotate ( "text" , x = r.tol - 0.05 , y = 0.75 , label = r.tol.label, colour = "darkred" ) 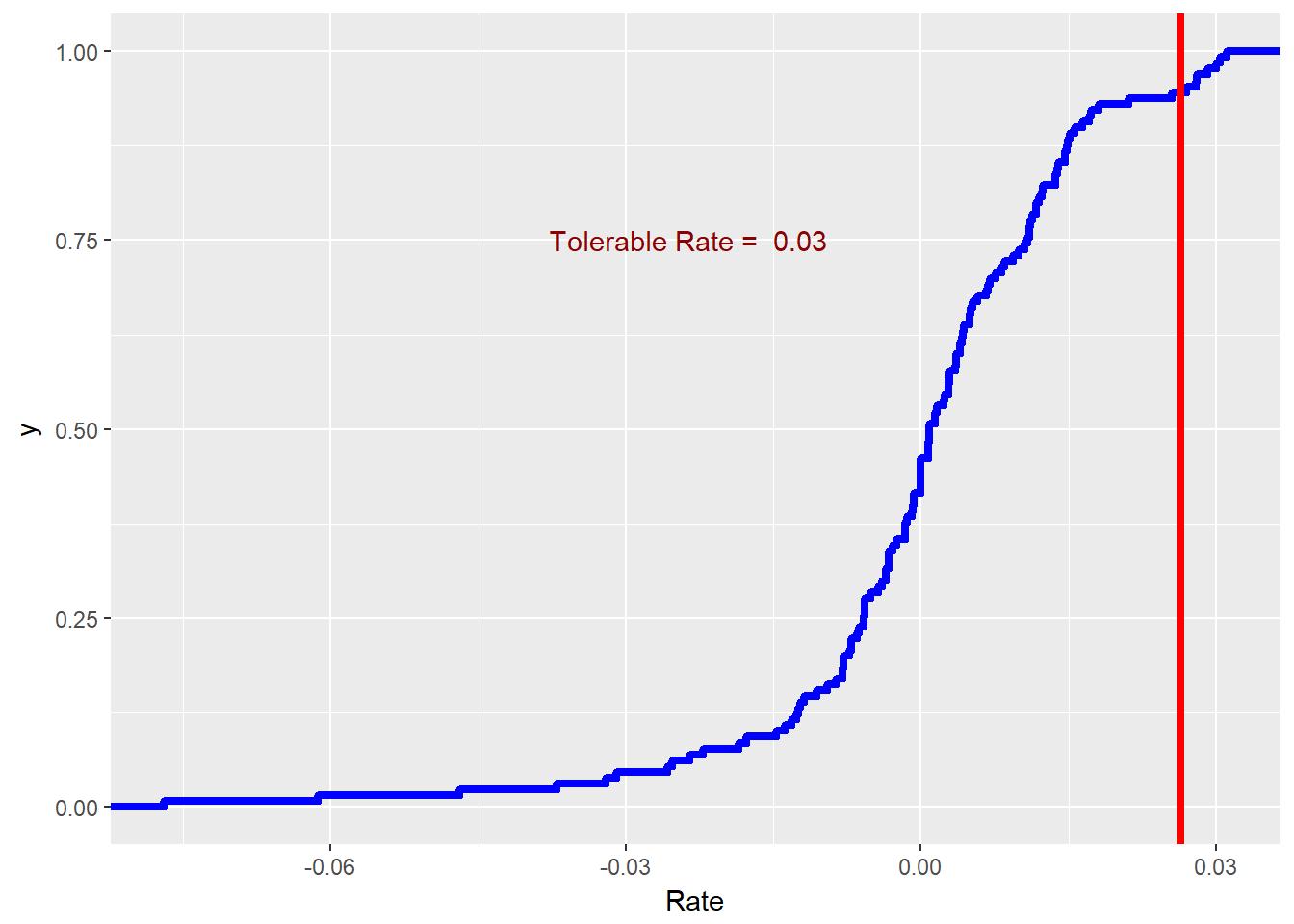
Ini mungkin sedikit lebih banyak daripada yang kita tawar pada awalnya. Kami menggunakan fungsi
paste dan round (ke dua, 2 , tempat desimal) untuk membuat label.Kami membuat garis yang lebih tebal ( size = 1.5 ). Pada 2% kami menggambar garis dengan geom_vline() dan menjelaskannya dengan teks.Sekarang kami telah membuat beberapa distribusi dari data langsung, mari kita perkirakan parameter distribusi tertentu yang mungkin sesuai dengan data itu.
3.5 Optimasi
Optimalisasi yang akan kami lakukan di sini membantu kami menemukan distribusi yang paling sesuai dengan data. Kami akan menggunakan hasil dari optimasi untuk mensimulasikan data itu untuk membantu kami mengambil keputusan secara prospektif .
Ada banyak distribusi di
R ?distributions akan memberi tahu Anda semua tentang mereka.- Jika
nameadalah nama distribusi (misalnya,normuntuk "normal"), maka
- dname = probabilitas d ensity (jika kontinu) atau probabilitas fungsi massa
name(pdf atau pmf), pikirkan "histogram" - pname = fungsi robability p kumulatif (CDF), pikirkan "s-curve"
- qname = fungsi q uantile (kebalikan dari CDF), “think line toleransi”
- rname = menggambar nomor r danom dari
name(argumen pertama selalu jumlah undian), pikirkan apa pun yang Anda inginkan ... itu agak acak
- Dan cara menulis sendiri (seperti distribusi
paretokami gunakan dalam keuangan)
3.5.1 Cobalah latihan ini
Misalkan seri harga
EIUR adalah tolok ukur dalam beberapa kontrak impor yang Anda tulis sebagai petugas pengadaan organisasi Anda. Kekhawatiran Anda adalah volatilitas.Dengan demikian Anda berpikir bahwa Anda perlu mensimulasikan ukuran harga harga, apa pun arahnya. Gambar histogram nilai absolut dari tarif harga. require (ggplot2) r.tol <- quantile (xmprice.r.df $ Rate, 0.95 ) r.tol.label <- paste ( "Tolerable Rate = " , round (r.tol, 2 )) ggplot (xmprice.r.df, aes (Rate.abs)) + geom_histogram ( fill = "cornsilk" , colour = "grey60" ) + geom_density () + geom_vline ( xintercept = r.tol, colour = "red" , size = 1.5 ) + annotate ( "text" , x = 0.055 , y = 30 , label = r.tol.label, colour = "darkred" ) 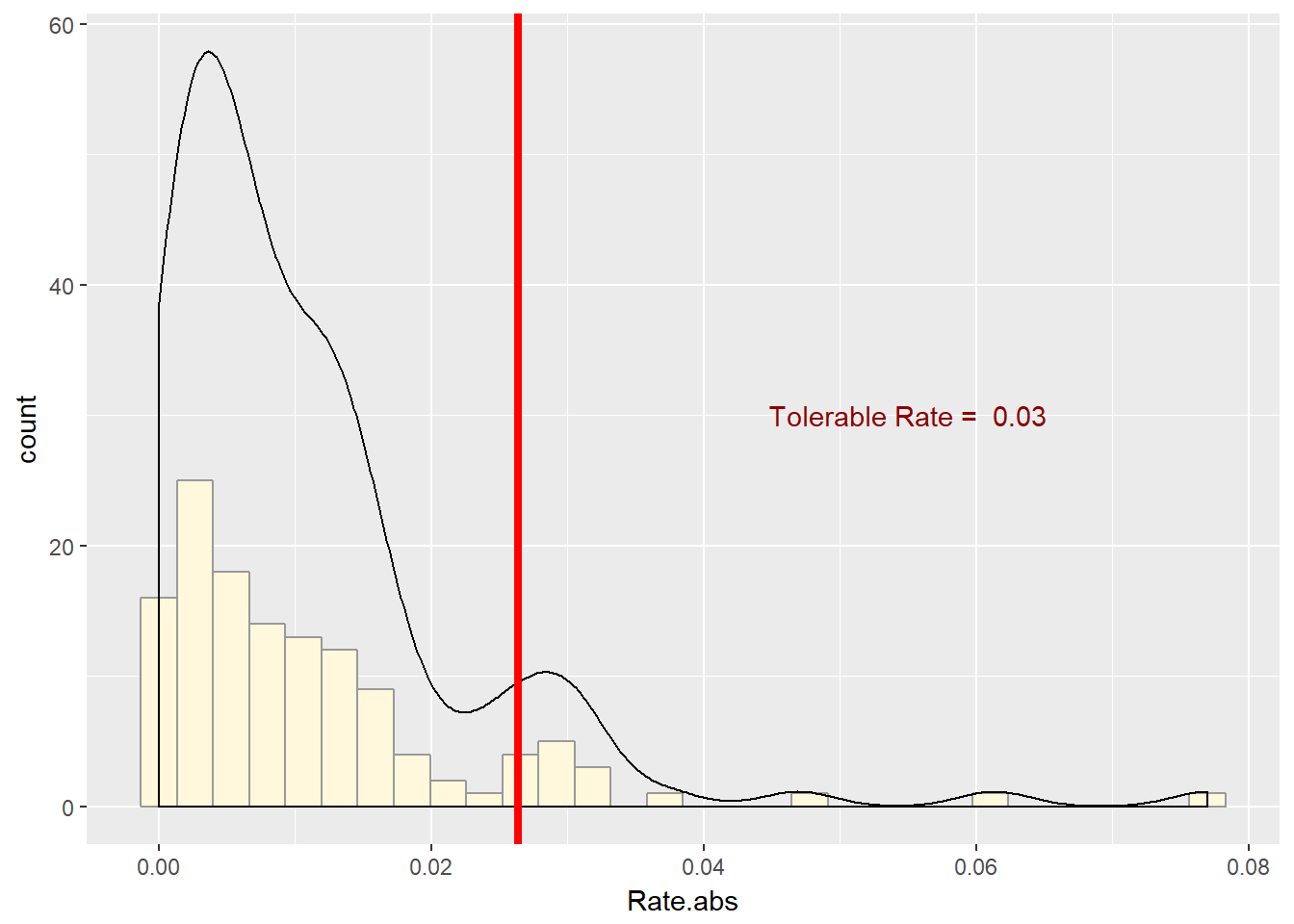
Seri ini miring kanan dan berekor tebal. Kami akan menggunakan fungsi ini untuk menyatukan beberapa perhitungan statistik.
## r_moments function INPUTS: r vector ## OUTPUTS: list of scalars (mean, sd, ## median, skewness, kurtosis) data_moments <- function (data) { require (moments) mean.r <- mean (data) sd.r <- sd (data) median.r <- median (data) skewness.r <- skewness (data) kurtosis.r <- kurtosis (data) result <- data.frame ( mean = mean.r, std_dev = sd.r, median = median.r, skewness = skewness.r, kurtosis = kurtosis.r) return (result) } Kita mungkin perlu
install.packages("moments") untuk membuat fungsi ini beroperasi. Kami kemudian menjalankan kalimat-kalimat ini. ans <- data_moments (xmprice.r.df $ Rate.abs) ans <- round (ans, 4 ) knitr :: kable (ans) | berarti | std_dev | median | kecondongan | kurtosis |
|---|---|---|---|---|
| 0,0109 | 0,0117 | 0,0074 | 2.523 | 12.1545 |
Seperti yang kita duga secara visual, seri ini condong ke kanan dan sangat tebal. Ini dapat menunjukkan bahwa fungsi
gamma dan pareto dapat membantu kami menggambarkan seri ini dan mempersiapkan kami untuk simulasi, estimasi, dan inferensi. Kami akan menggunakan fungsi fitdistr dari MASS dan kembali ke fungsi momen ini.3,6 Perkirakan sampai semangat meningkat ...
Kami akan mencoba satu metode yang cukup sering berhasil dalam praktiknya, Metode Momen ("MM" atau, yang lebih sayang, "MOM"). Teknik estimasi ini menemukan parameter distribusi sedemikian rupa sehingga momen-momen data cocok dengan momen-momen distribusi. Metode lain termasuk:
fitdistr: Biarkan kotak buram melakukan pekerjaan untuk Anda; lihat paketMASSyang menggunakan pendekatan "kemungkinan maksimum" dalam fungsi estimasifitdistr(sepertilmuntuk regresi).fitdistrplus: Untuk analis yang lebih berani, paket ini berisi beberapa metode, termasuk MM, untuk menyelesaikan pekerjaan.
karena kami percaya bahwa harga absolut entah bagaimana mengikuti distribusi
gamma . Anda dapat melihat distribusi ini dengan cukup mudah di artikel bagus Wikipedia tentang masalah ini. Di belakang adegan manajerial, kita dapat memodelkan kerugian dengan fungsi keparahan gamma yang memungkinkan kemiringan dan ekor "berat". Kita dapat menentukan distribusi gamma dengan parameter shape, \ (\ alpha \) , dan scale, \ (\ beta \) . Kami akan menemukan dalam analisis kerugian operasional bahwa distribusi ini sangat berguna untuk kerugian sensitif waktu.Ternyata Kami dapat menentukan parameter bentuk dan skala menggunakan mean, \ (\ mu \) , dan standar deviasi, \ (\ sigma \) dari keparahan acak, \ (X \) . Parameter skala adalah \ [\ beta = \ sigma ^ 2 / \ mu, \] dan parameter bentuk,
\ [\ alpha = \ mu ^ 2 / \ sigma ^ 2. \]
Distribusi itu sendiri didefinisikan sebagai \ [f (x; alpha, \ beta) = \ frac {\ beta ^ {\ alpha} x ^ {\ alpha-1} e ^ {- x \ beta}} {\ Gamma (\ alpha)}, \] di mana, untuk memiliki pernyataan yang lengkap, \ [\ Gamma (x) = \ int_ {0} ^ {\ infty} x ^ {t-1} e ^ {- x} dx. \] Akhirnya mari kita implementasikan ke
RPertama, kami akan memuat sampel biaya dan menghitung momen dan parameter gamma:
cost <- read.csv ( "data/cost.csv" ) cost <- cost $ x cost.moments <- data_moments (cost) cost.mean <- cost.moments $ mean cost.sd <- cost.moments $ std_dev (cost.shape <- cost.mean ^ 2 / cost.sd ^ 2 ) ## [1] 19.06531 (cost.scale <- cost.sd ^ 2 / cost.mean) ## [1] 0.5575862 gamma.start <- c (cost.shape, cost.scale) Saat melakukan perhitungan ini, pastikan bahwa fungsi
data_moments dimuat ke ruang kerja.Kedua, kita dapat menggunakan
fitdistr dari paket Massuntuk memperkirakan parameter gamma alpha dan beta . require (MASS) fit.gamma.cost <- fitdistr (cost, "gamma" ) fit.gamma.cost ## shape rate ## 20.2998092 1.9095724 ## ( 2.3729250) ( 0.2259942) Ketiga, kami menyusun rasio estimasi dengan kesalahan estimasi standar. Ini menghitung jumlah standar deviasi yang jauh dari nol. Jika mereka "jauh" cukup jauh dari nol, kami memiliki alasan untuk menolak hipotesis nol bahwa estimasi tidak berbeda dari nol.
(cost.t <- fit.gamma.cost $ estimate / fit.gamma.cost $ sd) ## shape rate ## 8.554762 8.449652 knitr :: kable (cost.t) | bentuk | 8.554762 |
| menilai | 8.449652 |
Bagus ... tetapi kami juga mencatat bahwa parameter skala adalah
fit.gamma.cost$estimate[2] / gamma.start[2] dikali estimasi momen di atas.3.6.1 Cobalah latihan ini
Mari kita gunakan tingkat seri harga input-ekspor dan distribusi
t bukan gamma .Pertama, kami menghitung momen (rata-rata, dll.).
rate <- xmprice.r.df $ Rate rate.moments <- data_moments (rate) (rate.mean <- rate.moments $ mean) ## [1] 0.0004595748 (rate.sd <- rate.moments $ std_dev) ## [1] 0.01602021 Kedua, kami menggunakan
fitdistr dari paket Massuntuk memperkirakan parameter distribusi t . fit.t.rate <- fitdistr (rate, "t" , hessian = TRUE ) fit.t.rate ## ms df ## 0.001791738 0.009833018 2.888000806 ## (0.001059206) (0.001131725) (0.843729312) Ketiga, kami menyimpulkan apakah kami melakukan pekerjaan dengan baik atau tidak. Hipotesis nol adalah bahwa parameter tidak berbeda dari nol ( \ (H_0 \) ). Kami menghitung statistik t untuk memperkirakan pemetaan estimasi parameter ke skala tanpa dimensi yang akan menghitung jumlah standar deviasi dari hipotesis nol bahwa parameter hanya nol dan tidak digunakan lebih lanjut.
## ms df ## 1.691586 8.688522 3.422900 Bagus ... tapi parameter lokasi itu agak rendah relatif terhadap perkiraan momen. apa lagi yang bisa kita lakukan?Simulasikan hasil perkiraan dan lihat apakah, setidaknya, kemiringan dan kurtosis sejalan dengan momen.
3.7 Ringkasan
Kami menggunakan kemampuan kami yang baru ditemukan untuk menulis fungsi dan membangun gambar distribusi yang berwawasan luas. Kami juga menjalankan regresi nonlinier (gamma dan t-distribusi memang sangat nonlinier) menggunakan paket dan metode momen. Semua ini untuk menjawab pertanyaan bisnis kritis.
Lebih khusus lagi kami memasuki:
- Excel mirip proses: Tabel pivot dan VLOOKUP
- Excel mirip fungsinya
- Grafik untuk mendapatkan wawasan tentang distribusi
- Memperkirakan parameter distribusi
- Kebaikan bugar
3.8 Bacaan Lebih Lanjut
Berbagai bab Teetor memiliki banyak hal untuk membimbing kita dalam penulisan fungsi dan pembangunan ekspresi. Nilai sekarang dan tingkat pengembalian internal dapat ditemukan di Brealey et al. Penggunaan
ggplot2dalam bab ini sangat bergantung pada Chang (2014).3.9 Set Latihan
Praktik ini menetapkan bahan referensi yang dikembangkan dalam bab ini. Kami akan mengeksplorasi masalah dan data baru dengan model,
Rpaket, tabel, dan plot yang sudah dikerjakan dalam bab ini.3.9.1 Mengatur A
Dalam set ini kita akan membangun set data menggunakan filter
ifdan diffpernyataan. Kami kemudian akan menjawab beberapa pertanyaan menggunakan plot dan laporan tabel pivot. Kami kemudian akan meninjau fungsi untuk menampung pendekatan kami jika kami ingin menjalankan analisis yang sama pada set data lainnya.3.9.1.1 Masalah
Manajer rantai pasokan di perusahaan kami terus mencatat bahwa kami memiliki paparan signifikan terhadap harga minyak pemanas (Minyak Pemanasan No. 2, atau HO2), khususnya Pelabuhan New York. Paparan tersebut menyentuh biaya variabel untuk menghasilkan beberapa produk. Ketika HO2 volatile, demikian juga pendapatan. Perusahaan kami telah melewatkan perkiraan pendapatan selama lima kuartal berturut-turut. Untuk mendapatkan pegangan tentang Brent, kami mengunduh kumpulan data ini dan meninjau beberapa aspek dasar dari harga.
# Read in data HO2 <- read.csv ( "data/nyhh02.csv" , header = T, stringsAsFactors = F) # stringsAsFactors sets dates as # character type head (HO2) HO2 <- na.omit (HO2) ## to clean up any missing data str (HO2) # review the structure of the data so far 3.9.1.2 Pertanyaan
- Apa sifat pengembalian HO2? Kami ingin mencerminkan naik turunnya pergerakan harga, sesuatu yang sangat menarik bagi manajemen. Pertama, kami menghitung perubahan persentase sebagai pengembalian log. Minat kami adalah pasang surut. Untuk melihat itu kita menggunakan
ifdanelsepernyataan untuk mendefinisikan kolom baru yang disebutdirection. Kami akan membangun kerangka data untuk menampung analisis ini.
# Construct expanded data frame return <- as.numeric ( diff ( log (HO2 $ DHOILNYH))) * 100 size <- as.numeric ( abs (return)) # size is indicator of volatility direction <- ifelse (return > 0 , "up" , ifelse (return < 0 , "down" , "same" )) # another indicator of volatility date <- as.Date (HO2 $ DATE[ - 1 ], "%m/%d/%Y" ) # length of DATE is length of return +1: omit 1st observation price <- as.numeric (HO2 $ DHOILNYH[ - 1 ]) # length of DHOILNYH is length of return +1: omit first observation HO2.df <- na.omit ( data.frame ( date = date, price = price, return = return, size = size, direction = direction)) # clean up data frame by omitting NAs str (HO2.df) Kami dapat merencanakan dengan
ggplot2paket. Dalam ggplotpernyataan yang kami gunakan aes, "estetika", untuk memilih sumbu x(horizontal) dan y(vertikal). Gunakan group =1untuk memastikan bahwa semua data diplot. Yang ditambahkan ( +) geom_lineadalah metode geometris yang membangun plot garis.Mari kita coba grafik batang dari nilai absolut dari tingkat harga. Kami menggunakan
geom_baruntuk membangun gambar ini.Sekarang mari kita membangun overlay
returnpada size.- Mari kita menggali lebih dalam dan menghitung nilai mean, standar deviasi, dll. Memuat
data_moments()fungsinya. Jalankan fungsi menggunakanHO2.df$returnsubset dan tulisknitr::kable()laporan. - Mari berputar
sizedanreturnterusdirection. Berapa rata-rata dan kisaran pengembalian menurut arah? Seberapa sering kita melihat pergerakan positif atau negatif dalam HO2?
3.9.2 Mengatur B
Kami akan menggunakan data dari set sebelumnya untuk menyelidiki distribusi pengembalian yang kami hasilkan. Ini akan memerlukan pemasangan data ke beberapa distribusi parametrik serta merencanakan dan membangun kerangka data pendukung.
3.9.2.1 Masalah
Kami ingin lebih mengkarakterisasi distribusi gerakan naik dan turun secara visual. Kami juga ingin mengulangi analisis secara berkala untuk dimasukkan dalam laporan manajemen.
3.9.2.2 Pertanyaan
- Bagaimana kita dapat menunjukkan perbedaan dalam bentuk naik turunnya HO2, terutama mengingat toleransi kita terhadap risiko? Mari kita gunakan
HO2.dfframe data denganggplot2dan fungsi frekuensi relatif kumulatifstat_ecdf. - Bagaimana kita bisa secara teratur, dan andal, menganalisis pergerakan harga HO2? Untuk persyaratan ini, mari kita menulis fungsi yang mirip dengan
data_moments.
Ayo tes
HO2_movement().Semangat: lebih banyak pekerjaan hari ini (membangun fungsi) berarti lebih sedikit pekerjaan besok (tulis laporan lain).
- Misalkan kita ingin mensimulasikan pergerakan masa depan dalam pengembalian HO2. Distribusi apa yang mungkin kita gunakan untuk menjalankan skenario itu? Di sini, mari kita gunakan fungsi
MASSpaketfitdistr()untuk menemukan kecocokan optimal dari data HO2 ke distribusi parametrik.
3.9.3 Berlatih Mengatur Pembukaan
- Sebutkan keterampilan R yang dibutuhkan untuk menyelesaikan set latihan ini.
- Paket apa yang digunakan untuk menghitung dan membuat grafik hasil. Jelaskan masing-masing.
- Seberapa baik hasil mulai menjawab pertanyaan bisnis yang diajukan pada awal setiap praktik?
3.10 Proyek
3.10.1 Latar Belakang
Perusahaan Anda menggunakan gas alam sebagai input utama untuk mendaur ulang limbah yang tidak dapat dipulihkan. Satu-satunya hal yang mencegah operasi menjadi sedikit lebih baik daripada titik impas adalah harga gas alam yang tidak stabil. Dalam tinjauan tahunannya, manajemen memerlukan informasi dan analisis operasi daur ulang dengan maksud untuk membuat keputusan tentang kontrak outsourcing. Kontrak ini biasanya memiliki tenor tiga tahun.
Karena manajemen akan membuat atau melakukan outsourcing keputusan dalam jangka waktu tiga tahun ke depan, analis akan membangun model yang menggambarkan pergerakan historis dalam harga gas alam, volatilitas harga-harga itu, dan distribusi probabilitas untuk mensimulasikan skenario gas alam di masa depan.
3.10.2 Data
Dalam analisis pendahuluan, Anda mengumpulkan data dari FRED tentang harga gas alam harian. Anda akan menggunakan data ini untuk mengkarakterisasi pergerakan historis harga gas bumi dan membangun distribusi probabilitas sementara untuk pembuatan skenario ke depan.
3.10.3 Alur Kerja
- Pengumpulan data. Kumpulkan, bersihkan, dan tinjau definisi data, dan transformasi data harga menjadi pengembalian. Gunakan tabel dan grafik untuk melaporkan hasil.
- Analisis.
- Kelompokkan harga ke atas, sama (tanpa pergerakan), dan turun menggunakan persentase perubahan harga harian sebagai kriteria.
- Buat tabel statistik ringkasan yang memutar data dan menghitung metrik.
- Buat grafik probabilitas kumulatif kelompok pengembalian historis yang naik, sama, dan turun.
- Estimasi parameter distribusi t Student untuk pergerakan naik, sama, dan turun dalam pengembalian gas bumi.
- Pengamatan dan Rekomendasi.
- Ringkas data, karakteristiknya, dan penerapannya untuk mengatasi masalah yang sedang dipecahkan untuk manajemen.
- Diskusikan hal-hal penting yang dapat diambil dari hasil analisis yang relevan dengan keputusan yang akan diambil manajer.
- Menghasilkan
R Markdowndokumen dengan potongan kode untuk mendokumentasikan dan menafsirkan hasil. - Format tersebut akan memperkenalkan masalah yang akan dianalisis, dengan bagian yang membahas data yang digunakan, dan yang mengikuti alur kerja.
3.10.4 Penilaian
Kami akan menggunakan rubrik berikut untuk menilai kinerja kami dalam memproduksi produk kerja analitik untuk pembuat keputusan.
- Teks ditata dengan rapi, dengan pembagian dan transisi yang jelas antara bagian dan sub-bagian. Tulisan itu sendiri terorganisir dengan baik, bebas dari kesalahan tata bahasa dan mekanis lainnya, dibagi menjadi kalimat lengkap, secara logis dikelompokkan ke dalam paragraf dan bagian, dan mudah diikuti dari tingkat pengetahuan yang diperkirakan.
- Semua hasil numerik atau ringkasan dilaporkan dengan presisi yang sesuai, dan dengan pengukuran ketidakpastian yang sesuai jika berlaku.
- Semua gambar dan tabel yang ditampilkan relevan dengan argumen untuk kesimpulan akhir. Gambar dan tabel mudah dibaca, dengan keterangan informatif, judul, label sumbu dan legenda, dan ditempatkan di dekat potongan teks yang relevan.
- Kode diformat dan diatur sehingga mudah dibaca dan dipahami orang lain. Itu indentasi, komentar, dan menggunakan nama yang bermakna. Ini hanya mencakup perhitungan yang sebenarnya diperlukan untuk menjawab pertanyaan analitis, dan menghindari redundansi. Kode yang dipinjam dari catatan, dari buku, atau dari sumber yang ditemukan online secara eksplisit diakui dan bersumber di komentar. Fungsi atau prosedur yang tidak langsung diambil dari catatan memiliki tes yang menyertainya yang memeriksa apakah kode melakukan apa yang seharusnya. Semua kode berjalan, dan
R Markdownfileknitskepdf_documentoutput, atau output lain setuju dengan instruktur. - Spesifikasi model dijelaskan dengan jelas dan detail yang sesuai. Ada penjelasan yang jelas tentang bagaimana memperkirakan model membantu menjawab pertanyaan analitis, dan alasan untuk semua pilihan pemodelan. Jika beberapa model dibandingkan, mereka semua dijelaskan dengan jelas, bersama dengan alasan untuk mempertimbangkan beberapa model, dan alasan untuk memilih satu model di atas yang lain, atau untuk menggunakan beberapa model secara bersamaan.
- Estimasi aktual dan simulasi parameter model atau fungsi estimasi secara teknis benar. Semua perhitungan berdasarkan perkiraan dijelaskan dengan jelas, dan secara teknis juga benar. Semua estimasi atau jumlah yang diturunkan disertai dengan ukuran ketidakpastian yang tepat.
- Pertanyaan substantif, analitis semua dijawab setepat yang dimungkinkan oleh data dan model. Rantai penalaran dari hasil estimasi tentang model, atau jumlah yang diturunkan, hingga kesimpulan substantif jelas dan meyakinkan. Jawaban kontinjensi (misalnya, “jika X, maka Y, tetapi jika A, maka B, selain C”) juga dijelaskan sebagai dijamin oleh model dan data. Jika ketidakpastian dalam data dan model berarti jawaban untuk beberapa pertanyaan harus tidak tepat, ini juga tercermin dalam kesimpulan.
- Semua sumber yang digunakan, baik dalam percakapan, cetak, online, atau terdaftar dan diakui di mana mereka digunakan dalam kode, kata-kata, gambar, dan komponen analisis lainnya.
3.11 Referensi
Brealey
Chang
Teetor
rajutan
xts
kebun binatang
BLS




