Analisis Data Keuangan Mikro
4.1 Bayangkan Ini
Perusahaan Anda yang berbasis di AS baru saja mendapatkan kontrak senilai lebih dari 20 persen dari pendapatan perusahaan Anda saat ini di Spanyol. Sekarang semua orang telah pulih dari kudeta ini, manajemen Anda menginginkannya
- Ambil dan mulai menganalisis data tentang ekonomi Spanyol
- Bandingkan dan kontraskan pasar saham Spanyol dan nilai utang yang dikeluarkan pemerintah versus Amerika Serikat dan beberapa negara lain
- Mulailah membuat skenario ekonomi berdasarkan peristiwa politik yang mungkin, atau mungkin tidak, terjadi di Spanyol
Hingga saat ini kami telah meninjau beberapa cara untuk memanipulasi data dalam
R Kami kemudian meninjau beberapa konsep keuangan dan statistik dasar dalam RKami juga mendapat gagasan tentang alur kerja analitik keuangan.- Keputusan apa yang kita buat?
- Apa pertanyaan bisnis utama yang kita butuhkan untuk mendukung keputusan ini?
- Data apa yang kita butuhkan?
- Alat apa yang kita butuhkan untuk menganalisis data?
- Bagaimana kita mengkomunikasikan jawaban untuk menginformasikan keputusan?
4.1.1 Bekerja sebagai contoh
Mari kita gunakan alur kerja ini untuk memotivasi pekerjaan kita di bab ini.
- Mari kita mengidentifikasi keputusan di tempat kerja (misalnya, investasi dalam mesin baru, membiayai bangunan, mengakuisisi pelanggan, merekrut karyawan berbakat, mencari pabrik).
- Untuk keputusan ini, kami akan mencantumkan tiga pertanyaan bisnis yang Anda butuhkan untuk menginformasikan keputusan yang kami pilih.
- Sekarang kami mempertimbangkan data, kami mungkin perlu menjawab salah satu pertanyaan itu dan memilih dari rangkaian ini:
- Data ekonomi makro: PDB, inflasi, upah, populasi
- Data keuangan: harga pasar saham, harga obligasi, nilai tukar, harga komoditas
Berikut adalah contoh menggunakan skenario yang memulai bab ini.
- Keputusan kami adalah memasok segmen pasar baru
- Produk: perangkat tegangan dengan perangkat lunak pendukung
- Geografi: Spanyol
- Pelanggan: pembeli utama di Iberdrola, Repsol, dan Endesa
- Kami mengajukan tiga pertanyaan bisnis:
- Bagaimana kinerja perusahaan-perusahaan ini mempengaruhi ukuran dan waktu pemesanan?
- Bagaimana nilai produk mereka akan memengaruhi nilai bisnis kita dengan perusahaan-perusahaan ini?
- Kami adalah perusahaan mata uang fungsional AS (lihat FAS 52), jadi bagaimana kami mengelola pemulangan piutang yang berasal dari Spanyol?
- Beberapa data dan analisis untuk menginformasikan keputusan dapat mencakup
- Harga saham pelanggan: volatilitas dan korelasi
- Harga minyak: volatilitas
- Nilai tukar USD / EUR: volatilitas
- Secara keseluruhan: korelasi di antara indikator-indikator ini
4.1.2 Bagaimana kami akan melanjutkan
Bab ini akan mengembangkan fakta-fakta pasar yang menarik. Ini terus dipelajari dengan cara yang sulit: data keuangan tidak independen, ia memiliki volatilitas yang fluktuatif, dan ekstrem.
- Stok keuangan, obligasi, komoditas ... sebut saja ... memiliki hubungan yang sangat saling bergantung.
- Volatilitas jarang konstan dan sering memiliki struktur (pembalikan rata-rata) dan tergantung pada masa lalu.
- Guncangan di masa lalu tetap ada dan mungkin atau mungkin tidak lembab (bergoyang di kolam).
- Peristiwa ekstrem cenderung terjadi dengan peristiwa ekstrem lainnya.
- Pengembalian negatif lebih mungkin daripada pengembalian positif (condong ke kiri).
4.2 Membangun Fakta yang Bergaya
Contoh dari tahun 70-an, 80-an, dan 90-an memiliki banyak peristiwa global yang saling bersinggungan yang memengaruhi para pembuat keputusan. Kami akan memuat beberapa bantuan komputasi dan beberapa data dari Brent, memformat tanggal, dan membuat objek deret waktu (paket
zoo' will be needed by packages fBasics and evir`): library (fBasics) library (evir) library (qrmdata) library (zoo) data (OIL_Brent) str (OIL_Brent) ## An 'xts' object on 1987-05-20/2015-12-28 containing: ## Data: num [1:7258, 1] 18.6 18.4 18.6 18.6 18.6 ... ## - attr(*, "dimnames")=List of 2 ## ..$ : NULL ## ..$ : chr "OIL_Brent" ## Indexed by objects of class: [Date] TZ: UTC ## xts Attributes: ## NULL Kami akan menghitung tarif perubahan untuk harga minyak Brent berikutnya.
Brent.price <- as.zoo (OIL_Brent) str (Brent.price) ## 'zoo' series from 1987-05-20 to 2015-12-28 ## Data: num [1:7258, 1] 18.6 18.4 18.6 18.6 18.6 ... ## - attr(*, "dimnames")=List of 2 ## ..$ : NULL ## ..$ : chr "OIL_Brent" ## Index: Date[1:7258], format: "1987-05-20" "1987-05-21" "1987-05-22" "1987-05-25" "1987-05-26" ... Brent.return <- diff ( log (Brent.price))[ - 1 ] * 100 colnames (Brent.return) <- "Brent.return" head (Brent.return, n = 5 ) ## Brent.return ## 1987-05-22 0.5405419 ## 1987-05-25 0.2691792 ## 1987-05-26 0.1611604 ## 1987-05-27 -0.1611604 ## 1987-05-28 0.0000000 tail (Brent.return, n = 5 ) ## Brent.return ## 2015-12-21 -3.9394831 ## 2015-12-22 -0.2266290 ## 2015-12-23 1.4919348 ## 2015-12-24 3.9177726 ## 2015-12-28 -0.3768511 Mari kita lihat data ini dengan plot kotak dan fungsi autokorelasi. Petak kotak akan menunjukkan minimum hingga maksimum dengan rata-rata di tengah kotak. Plot autokorelasi akan mengungkapkan seberapa gigih pengembalian dari waktu ke waktu.
Kami menjalankan pernyataan ini.
boxplot ( as.vector (Brent.return), title = FALSE , main = "Brent Daily % Change" , col = "blue" , cex = 0.5 , pch = 19 ) skewness (Brent.return) kurtosis (Brent.return) Plot seri waktu ini menunjukkan banyak pengelompokan kembali dan lonjakan, terutama yang negatif.
Melakukan beberapa "bola mata ekonometrik" cluster ini tampaknya terjadi sekitar - Embargo minyak tahun 70-an - Ketinggian rezim suku bunga baru Paul Volcker di Fed - "kehancuran pasar saham" Black Monday "pada tahun 1987 - Teluk I - Barings dan bisnis turunan lainnya runtuh di tahun 90-an
- Mari kita lihat kemungkinan pengembalian positif versus negatif. Kami mungkin ingin meninjau definisi dan rentang skewness dan kurtosis untuk membantu kami.
Sekarang untuk melihat kegigihan:
acf ( coredata (Brent.return), main = "Brent Daily Autocorrelogram" , lag.max = 20 , ylab = "" , xlab = "" , col = "blue" , ci.col = "red" ) pacf ( coredata (Brent.return), main = "Brent Daily Partial Autocorrelogram" , lag.max = 20 , ylab = "" , xlab = "" , col = "blue" , ci.col = "red" ) Interval kepercayaan adalah garis putus-putus merah. ACF pada lag 6 berarti korelasi pengembalian Brent saat ini dengan pengembalian 6 hari perdagangan yang lalu, termasuk korelasi dari perdagangan hari 1 hingga 6. PACF lebih sederhana: itu adalah korelasi baku antara hari 0 dan hari 6. ACF dimulai pada lag 0 ( hari ini); PACF dimulai pada lag 1 (kemarin).
- Berapa hari perdagangan dalam minggu biasa atau dalam sebulan? Komentari paku (garis biru yang tumbuh di atas atau di bawah garis putus-putus merah).
- Seberapa tebal ekor itu?
Ini tampilan pertama:
boxplot ( as.vector (Brent.return), title = FALSE , main = "Brent Daily Returns" , col = "blue" , cex = 0.5 , pch = 10 ) 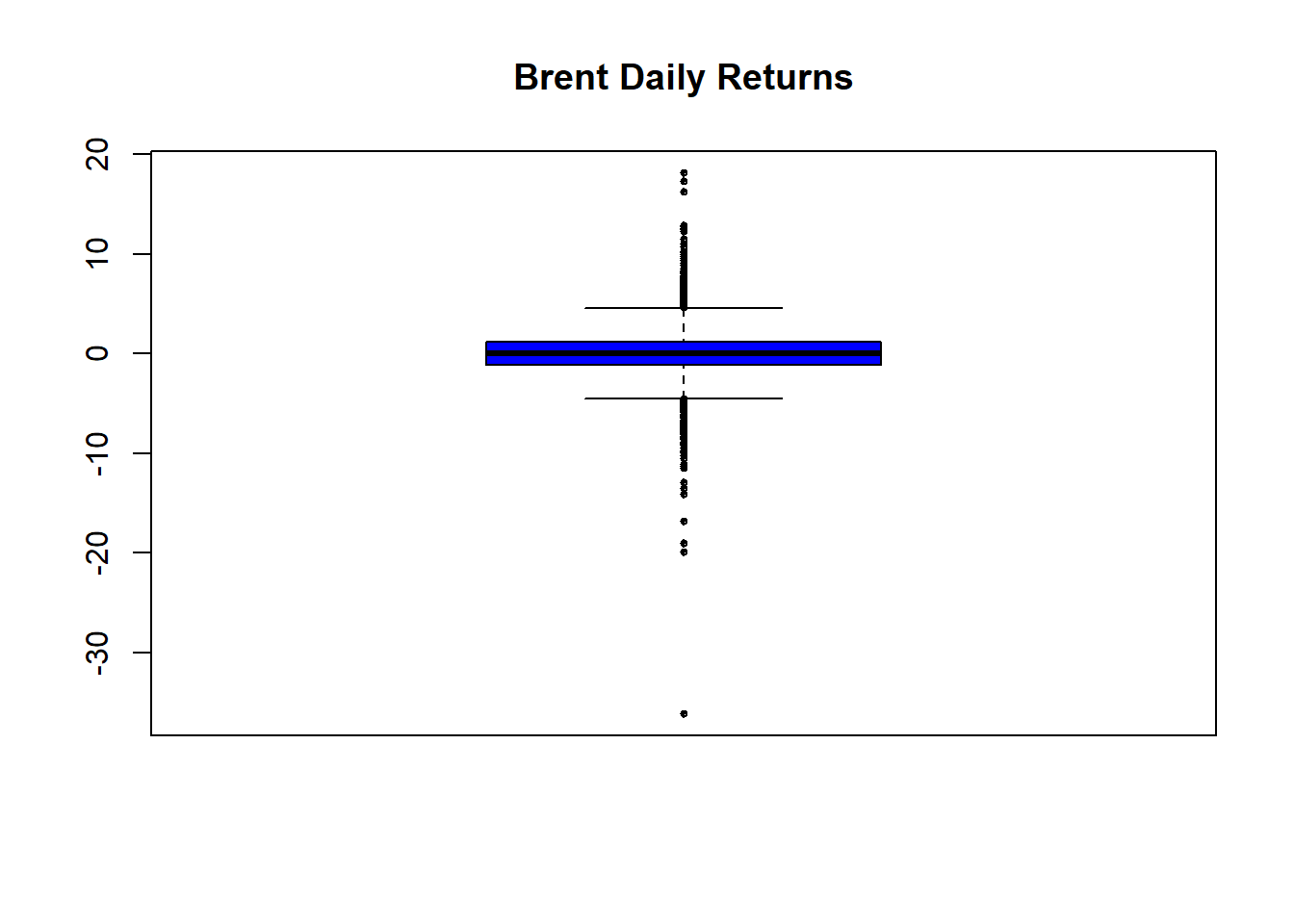
... dengan beberapa statistik dasar untuk mendukung ekonometrik bola mata dalam plot kotak:
skewness (Brent.return) ## [1] -0.6210447 ## attr(,"method") ## [1] "moment" kurtosis (Brent.return) ## [1] 14.62226 ## attr(,"method") ## [1] "excess" - Kemiringan negatif berarti ada lebih banyak pengamatan yang kurang dari median daripada yang lebih besar.
- Kurtosis setinggi ini berarti ekor yang cukup berat, terutama dalam pengembalian negatif. Itu berarti mereka lebih sering terjadi daripada pengembalian positif.
- Sebagian besar pengembalian negatif sering terjadi merupakan masalah bagi siapa pun yang memiliki aset ini.
4.2.1 Implikasi
- Kami harus merekomendasikan bahwa anggaran manajemen untuk badan distribusi dari rata-rata dan keluar ke tingkat positif.
- Pada saat yang sama, manajemen harus membuat buku pedoman yang komprehensif untuk kemungkinan kuat bahwa peristiwa bad tail sering terjadi dan mungkin terjadi lagi (dan mengapa tidak?).
- Sekarang untuk sesuatu yang sangat menarik
acf ( coredata (Brent.return), main = "Brent Autocorrelogram" , lag.max = 20 , ylab = "" , xlab = "" , col = "blue" , ci.col = "red" ) 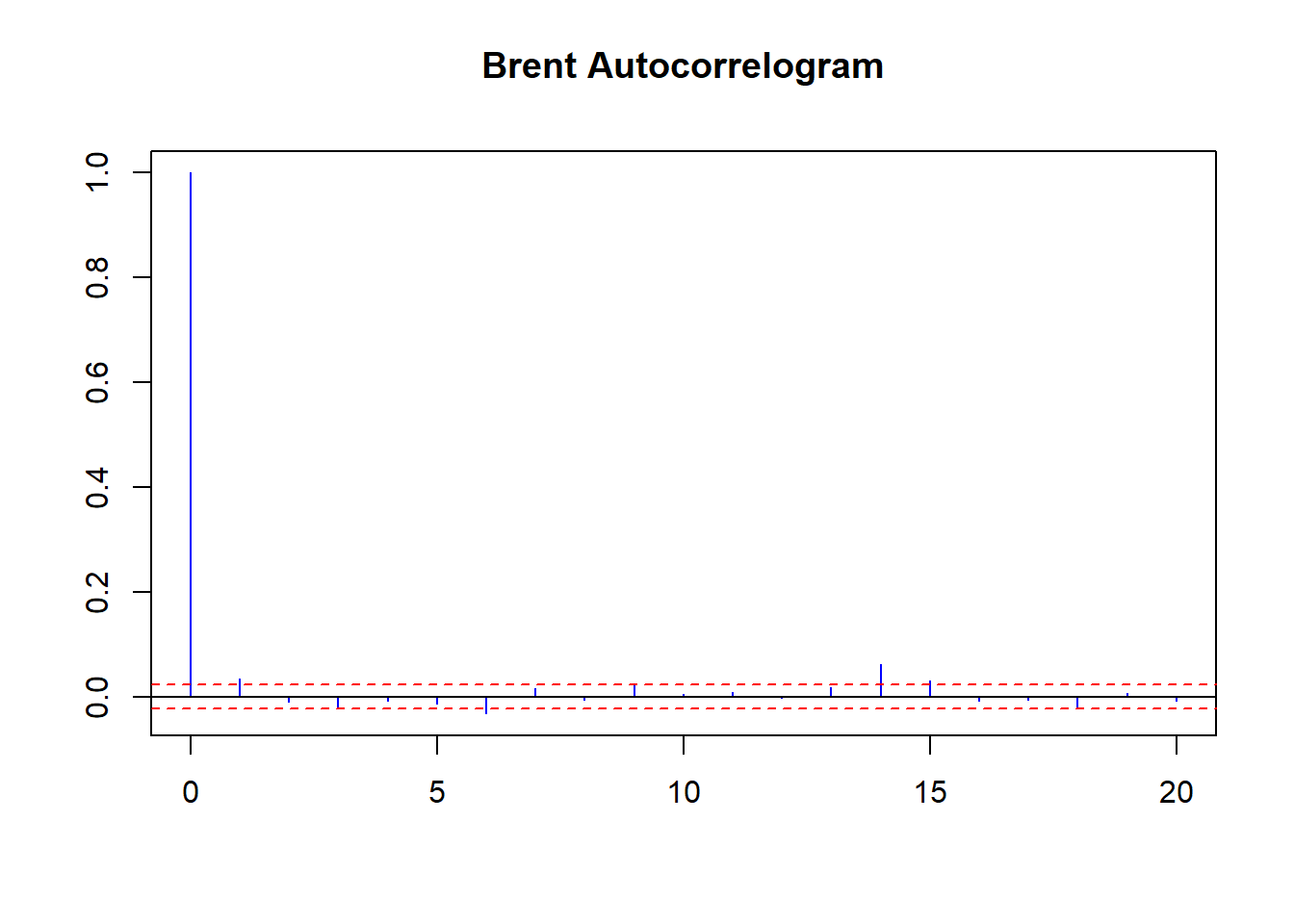
pacf ( coredata (Brent.return), main = "Brent Partial Autocorrelogram" , lag.max = 20 , ylab = "" , xlab = "" , col = "blue" , ci.col = "red" ) 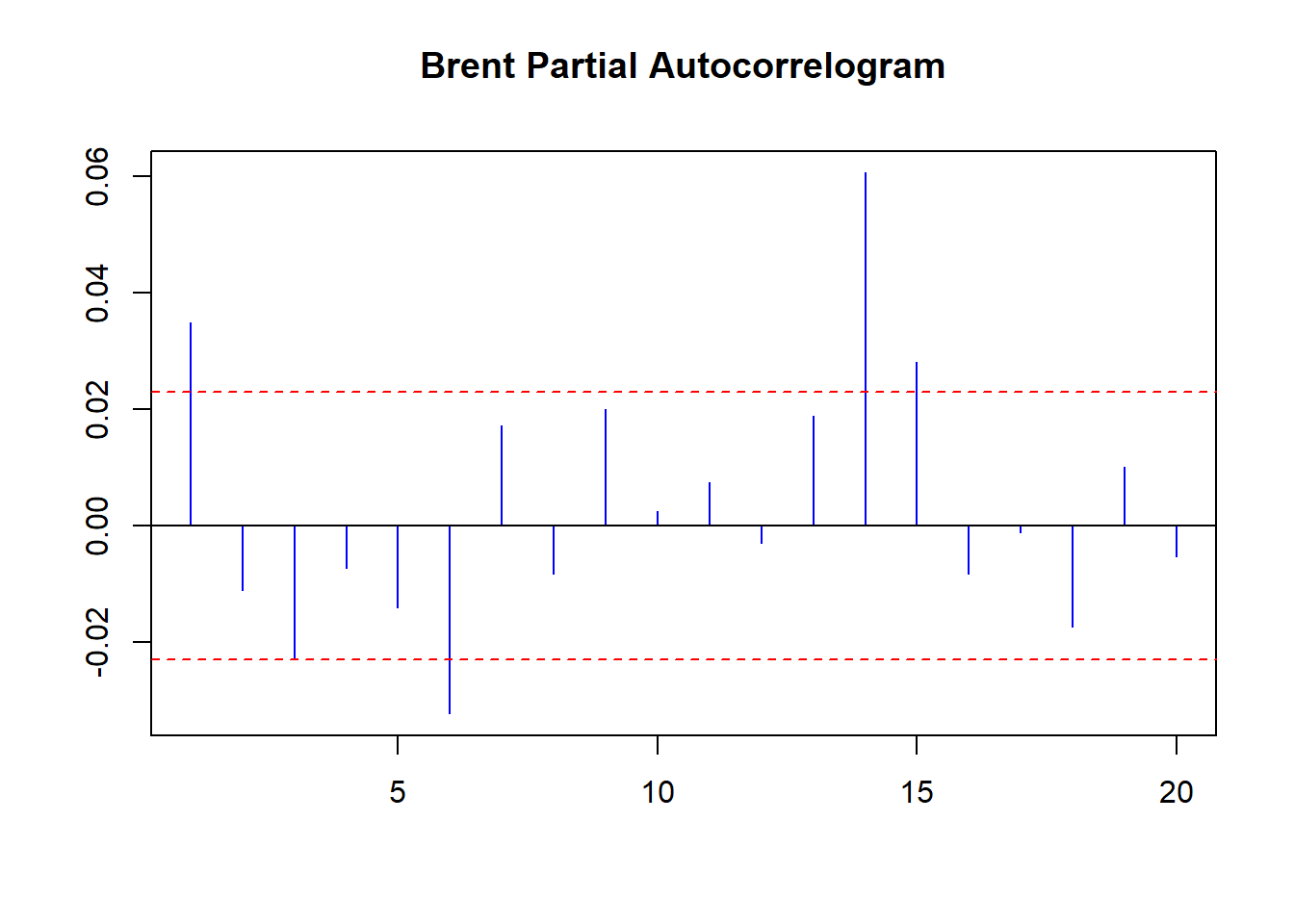
Rata-rata ada 5 hari dalam minggu perdagangan dan 20 dalam bulan perdagangan.
Beberapa pemikiran lebih lanjut:
- Tampaknya ada siklus bulanan mingguan dan negatif yang positif.
- Secara mingguan, harga negatif (5 hari perdagangan lalu) diikuti oleh harga negatif (hari ini) dan sebaliknya dengan harga positif.
- Secara bulanan, tarif negatif (20 hari yang lalu) diikuti oleh tarif positif (hari ini).
- Ada ingatan di pasar: korelasi positif setidaknya mingguan hingga sebulan lalu memperkuat tingkat negatif yang kuat dan sering terjadi (condong negatif dan leptokurtotik, alias ekor berat).
- Jalankan PACF selama 60 hari untuk melihat korelasi negatif 40 hari juga.
4.2.2 Sekarang untuk sesuatu yang sangat menarik ... lagi
Mari kita lihat ukuran pengembalian Brent. Nilai absolut dari pengembalian (pikirkan minyak dan negara-negara yang masuk dan meninggalkan UE!) Dapat menandakan penularan, mentalitas kawanan, dan panggilan margin yang sangat besar (dan jaminan untuk mendukung semuanya!).Mari kita jalankan kode ini:
Brent.return.abs <- abs (Brent.return) ## Trading position size matters Brent.return.tail <- tail (Brent.return.abs[ order (Brent.return.abs)], 100 )[ 1 ] ## Take just the first of the 100 ## observations and pick the first index <- which (Brent.return.abs > Brent.return.tail, arr.ind = TRUE ) ## Build an index of those sizes that ## exceed the heavy tail threshold Brent.return.abs.tail <- timeSeries ( rep ( 0 , length (Brent.return)), charvec = time (Brent.return)) ## just a lot of zeros we will fill up ## next Brent.return.abs.tail[index, 1 ] <- Brent.return.abs[index] ## A Phew! is in order Apa yang telah kita lakukan? Mari kita jalankan beberapa plot selanjutnya.
plot (Brent.return.abs, xlab = "" , main = "Brent Daily Return Sizes" , col = "blue" ) 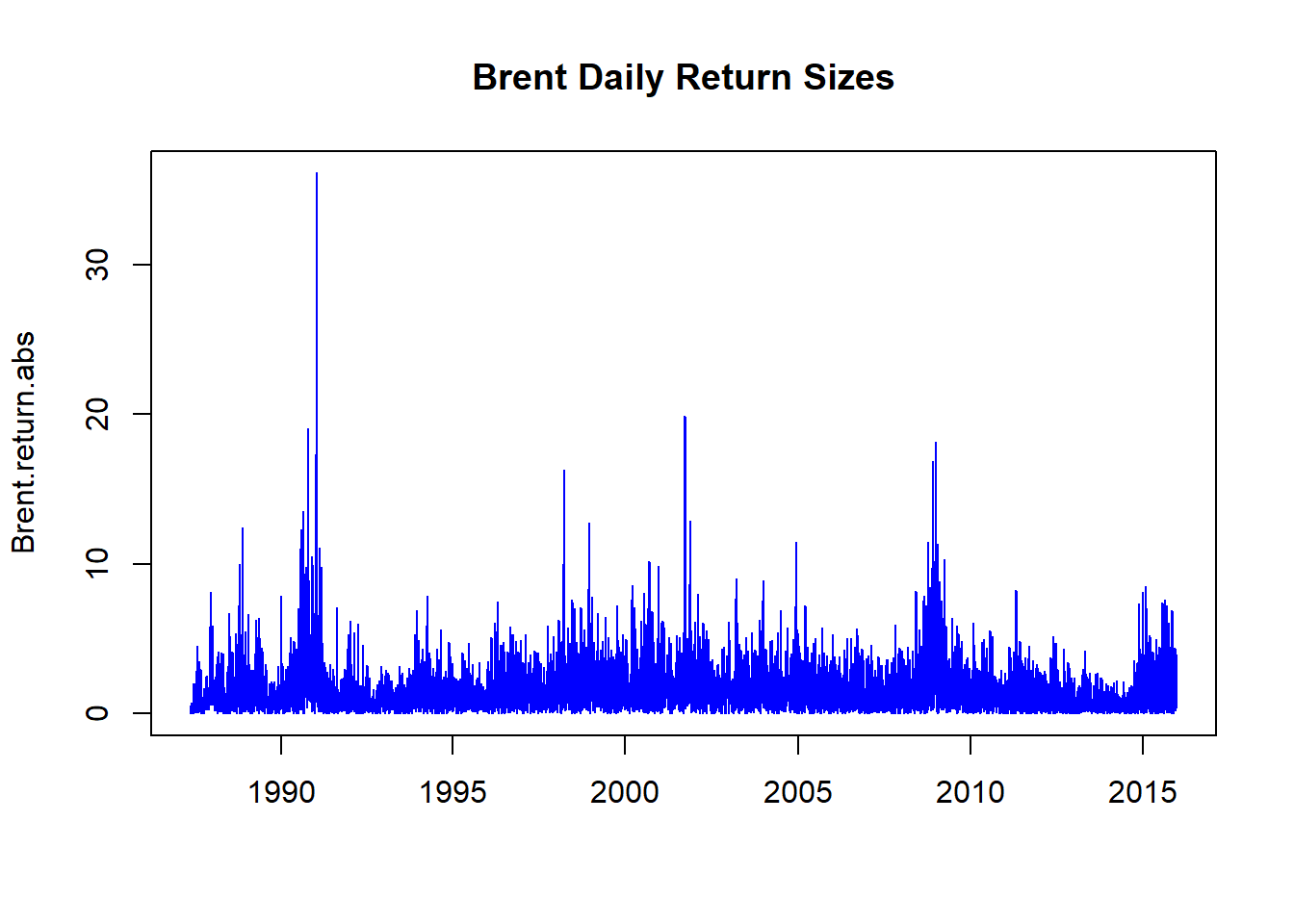
Kami melihat banyak volatilitas pengembalian - hanya dalam ukuran murni. Ini berkorelasi dengan inovasi keuangan dari tahun 80-an dan 90-an, serta Teluk 1, Teluk 2, Resesi Hebat, dan pendahulunya 9/11.
acf ( coredata (Brent.return.abs), main = "Brent Autocorrelogram" , lag.max = 60 , ylab = "" , xlab = "" , col = "blue" , ci.col = "red" ) 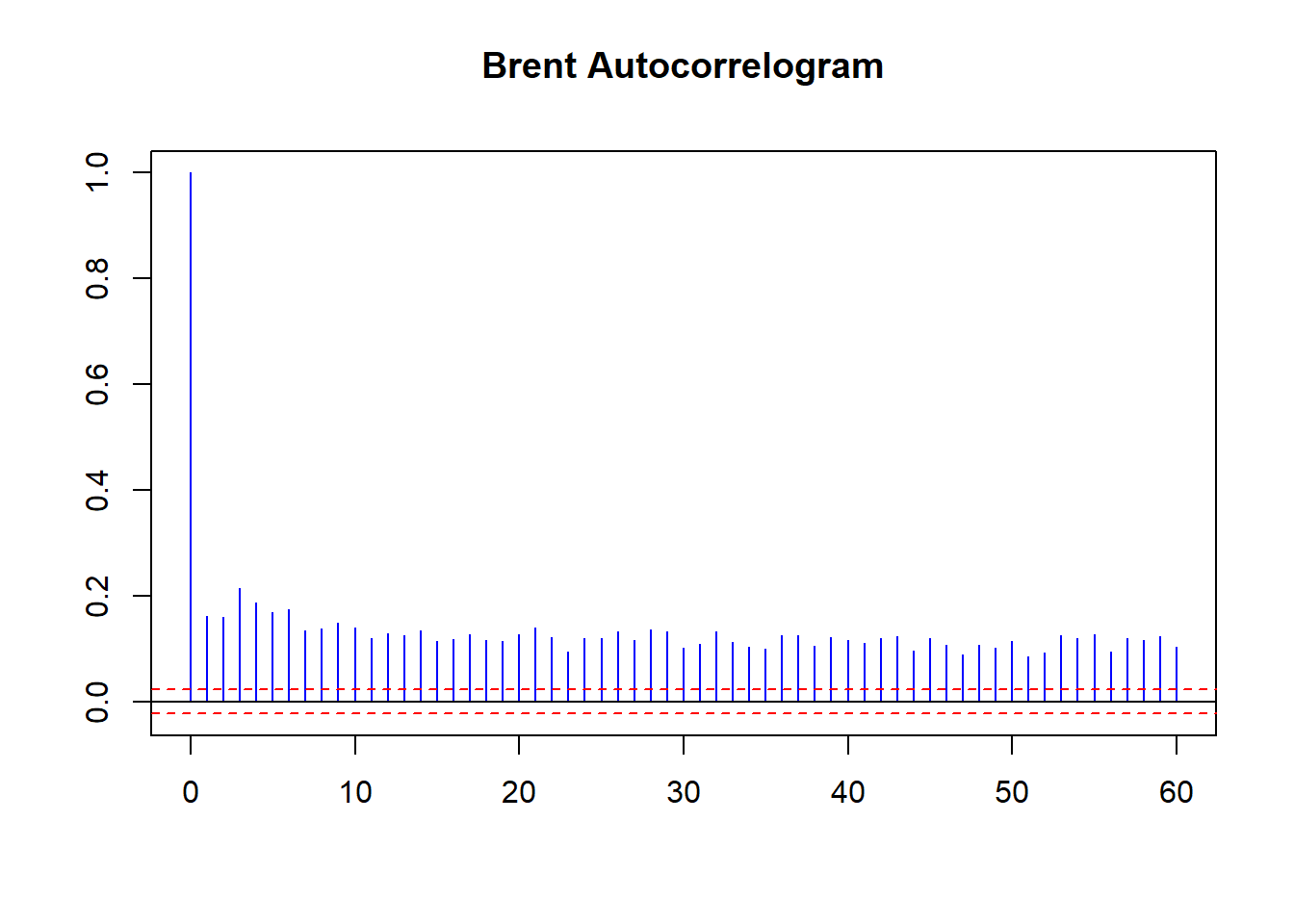
pacf ( coredata (Brent.return.abs), main = "Brent Partial Autocorrelogram" , lag.max = 60 , ylab = "" , xlab = "" , col = "blue" , ci.col = "red" ) 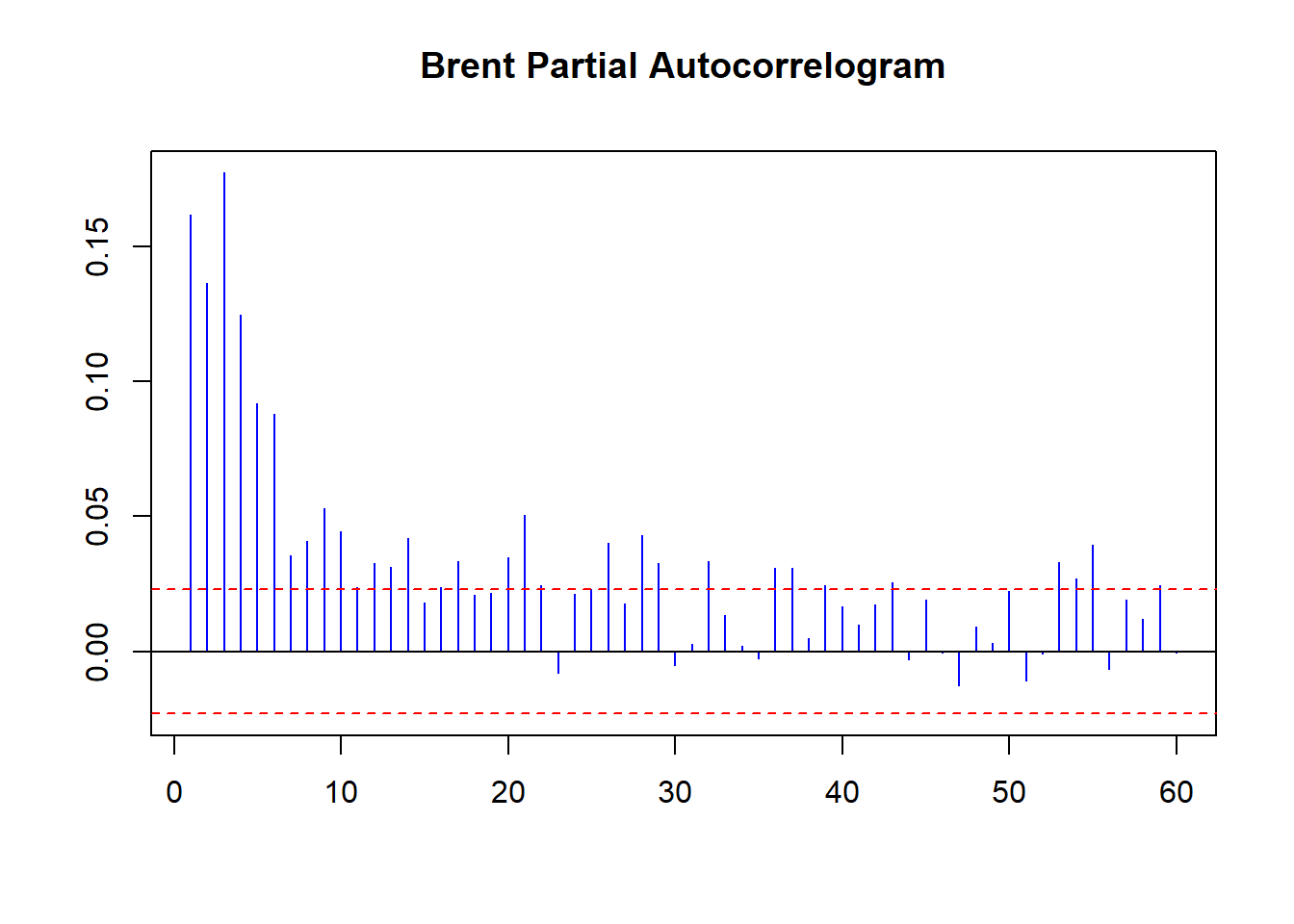
Ada Volatility Clustering berlimpah. Keterlambatan persisten yang kuat dari pengembalian absolut yang dibuktikan oleh plot
ACF . Ada bukti penurunan dengan setelah guncangan perdagangan terakhir 10 hari 10 lalu. Volatilitas bulanan mempengaruhi kinerja hari ini.Beberapa volatilitas ini muncul dari cara Brent diperdagangkan. Itu diangkat melalui kepala sumur di Laut Utara. Kemudian dijadwalkan untuk memuat ke kapal dan muatan kemudian menawar, bersama dengan rute ke tujuan.Dibutuhkan sekitar lima hari untuk memuat minyak mentah dan lima lainnya untuk menurunkan muatan. Pada setiap pemuatan dan pembongkaran sebagian, minyak mentah dinilai ulang. Lalu ada kelambatan pelayaran itu sendiri, di mana kertas mengklaim minyak mentah basah menciptakan harga lebih lanjut, dan volatilitas.
Selanjutnya kita mengeksplorasi hubungan antar variabel keuangan.
4.3 Terjebak dalam Persilangan Arus
Sekarang tugas kita adalah mengajukan pertanyaan yang sangat penting seputar konektivitas. Misalkan kita perbankan investasi kita di sektor-sektor ekonomi tertentu, dengan PDB, kemampuan keuangan, lapangan kerja, ekspor dan impor, dan sebagainya.
- Bagaimana kita memutuskan untuk melakukan kontrak barang dan jasa, vendor segmen, pelanggan segmen, berdasarkan interaksi ini?
- Bagaimana kita membangun portofolio peluang bisnis?
- Bagaimana kita mengidentifikasi risiko pemberontak dan relasional dan membangun buku pedoman untuk mengelola ini?
- Bagaimana perubahan dalam satu faktor sektor (katakanlah, keuangan, kemauan politik) mempengaruhi faktor-faktor di sektor lain?
Kami sekarang akan sedikit memperluas analisis univariat kami dan melihat korelasi silang untuk membantu kami mendapatkan kebenaran dasar di sekitar hubungan ini, dan mulai menjawab beberapa pertanyaan bisnis ini dalam konteks yang lebih spesifik.
Mari kita memuat perpustakaan
zoo dan qrmdata terlebih dahulu dan lihat kumpulan data EuroStoxx50 . Di sini kita dapat membayangkan bahwa kita sedang membangun kembali merek dan jejak kaki kita di Uni Eropa dan Inggris.Pelanggan kami mungkin perusahaan yang berbasis di negara-negara ini sebagai target pasar kami.- Data: 4 indeks bursa di seluruh Eropa (dan Inggris)
- Ini akan memungkinkan kami untuk membuat profil kemampuan maju dari perusahaan-perusahaan ini di seluruh ekonomi mereka.
- Sekali lagi kita akan melihat data pengembalian menggunakan rumus
diff(log(data))[-1].
require (zoo) require (qrmdata) require (xts) data ( "EuStockMarkets" ) EuStockMarkets.price <- as.zoo (EuStockMarkets) EuStockMarkets.return <- diff ( log (EuStockMarkets.price))[ - 1 ] * 100 Kami kemudian merencanakan tingkat harga dan pengembalian.
plot (EuStockMarkets.price, xlab = " " , main = " " ) 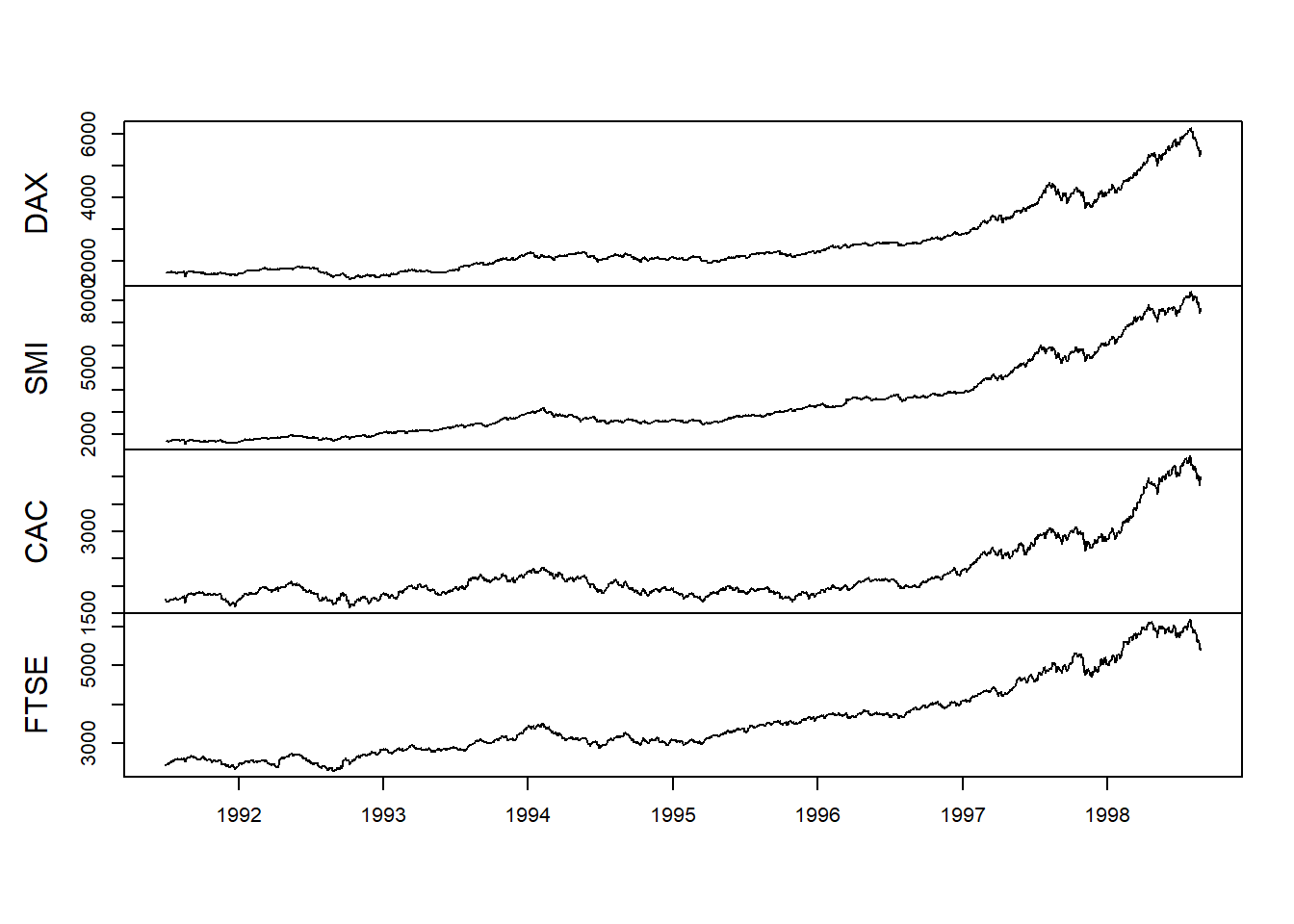
plot (EuStockMarkets.return, xlab = " " , main = " " ) 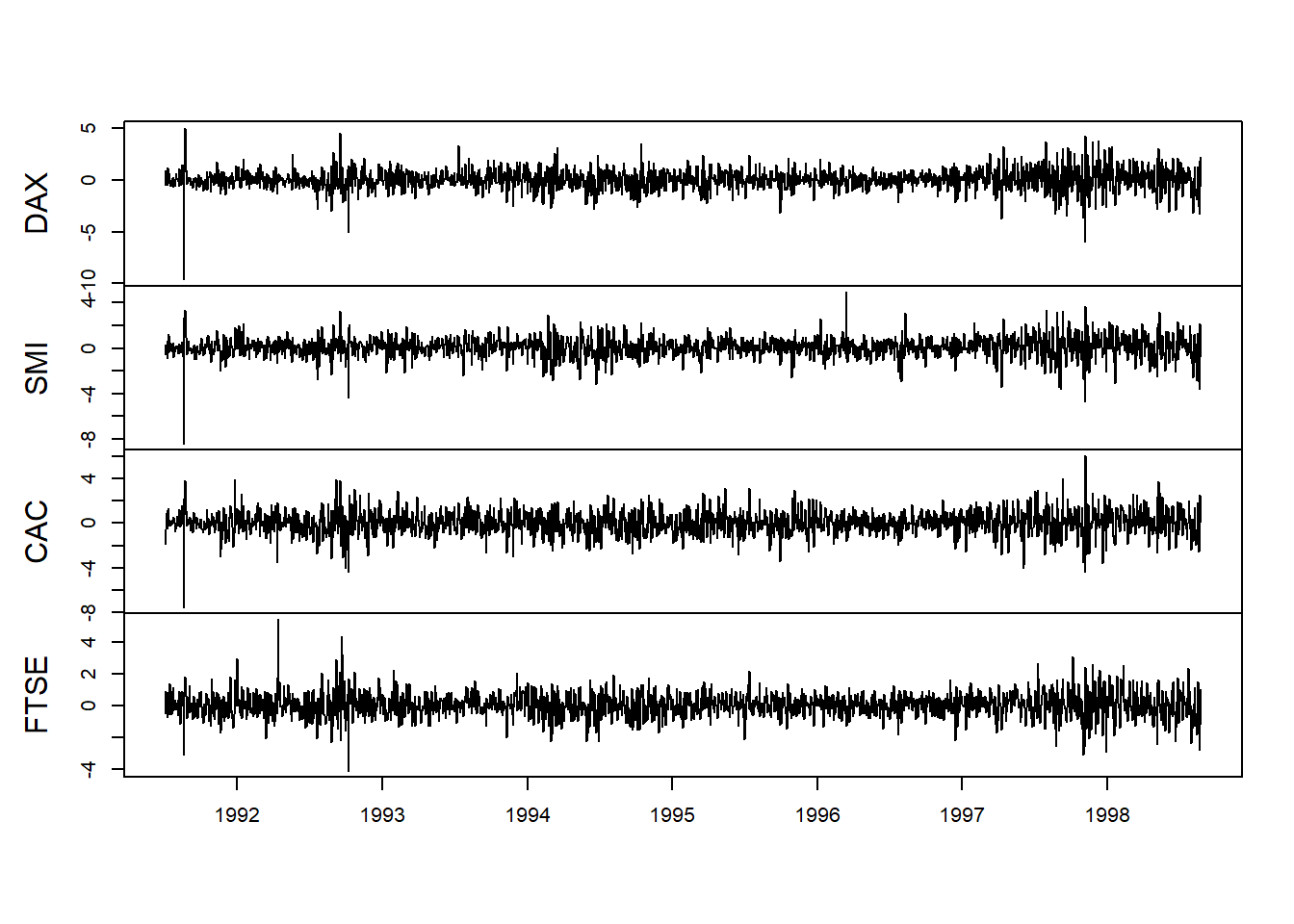
Kami melihat banyak hal yang sama seperti minyak Brent dengan pengelompokan volatilitas dan ekor yang sangat berbobot.
Mari kita lihat korelasi silang di antara sepasang indeks ini untuk melihat bagaimana mereka terkait lintas waktu (lag) untuk pengembalian dan nilai absolut pengembalian. Fungsi
ccf akan sangat membantu kami. ccf (EuStockMarkets.return[, 1 ], EuStockMarkets.return[, 2 ], main = "Returns DAX vs. CAC" , lag.max = 20 , ylab = "" , xlab = "" , col = "blue" , ci.col = "red" ) 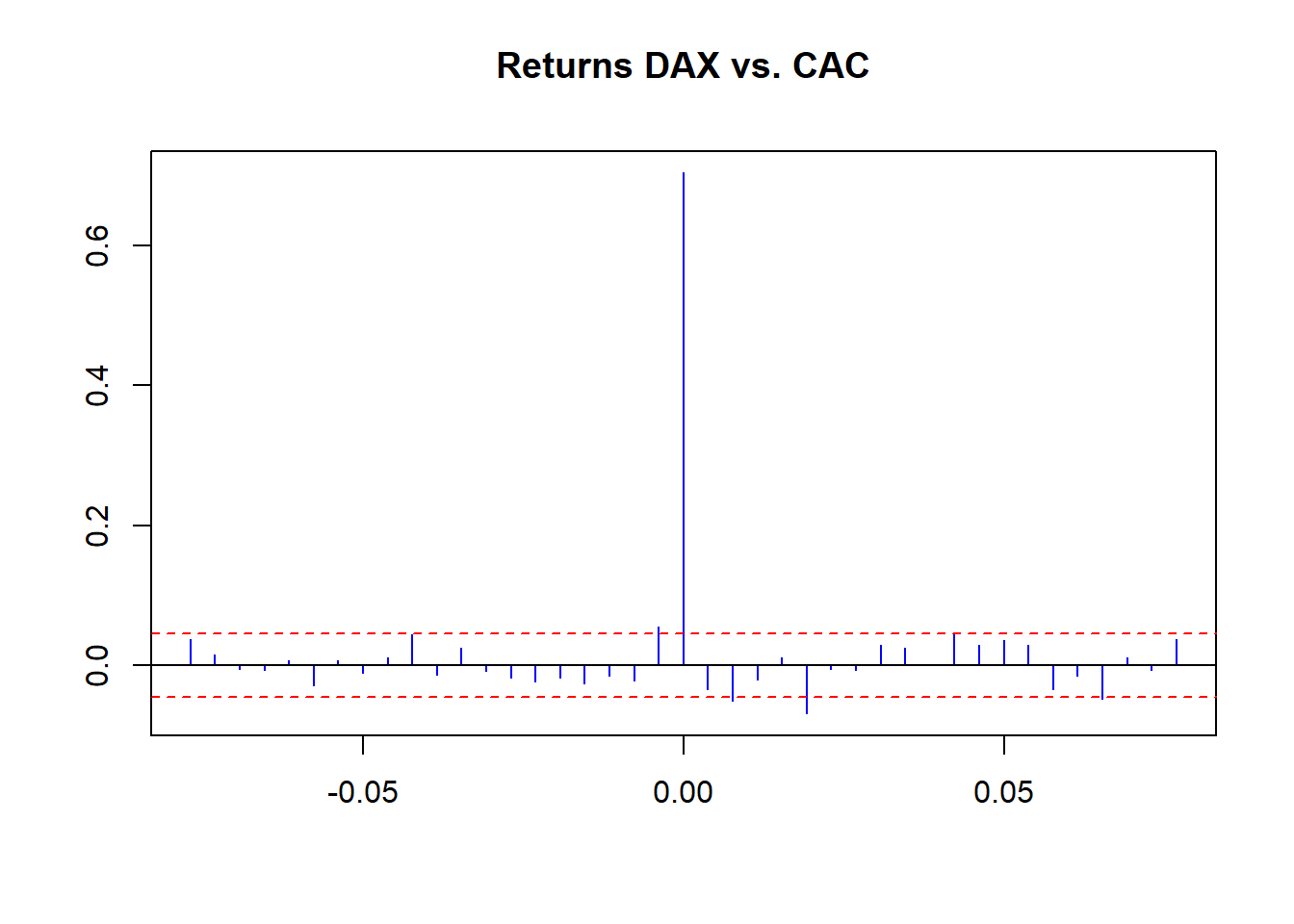
ccf ( abs (EuStockMarkets.return[, 1 ]), abs (EuStockMarkets.return[, 2 ]), main = "Absolute Returns DAX vs. CAC" , lag.max = 20 , ylab = "" , xlab = "" , col = "blue" , ci.col = "red" ) 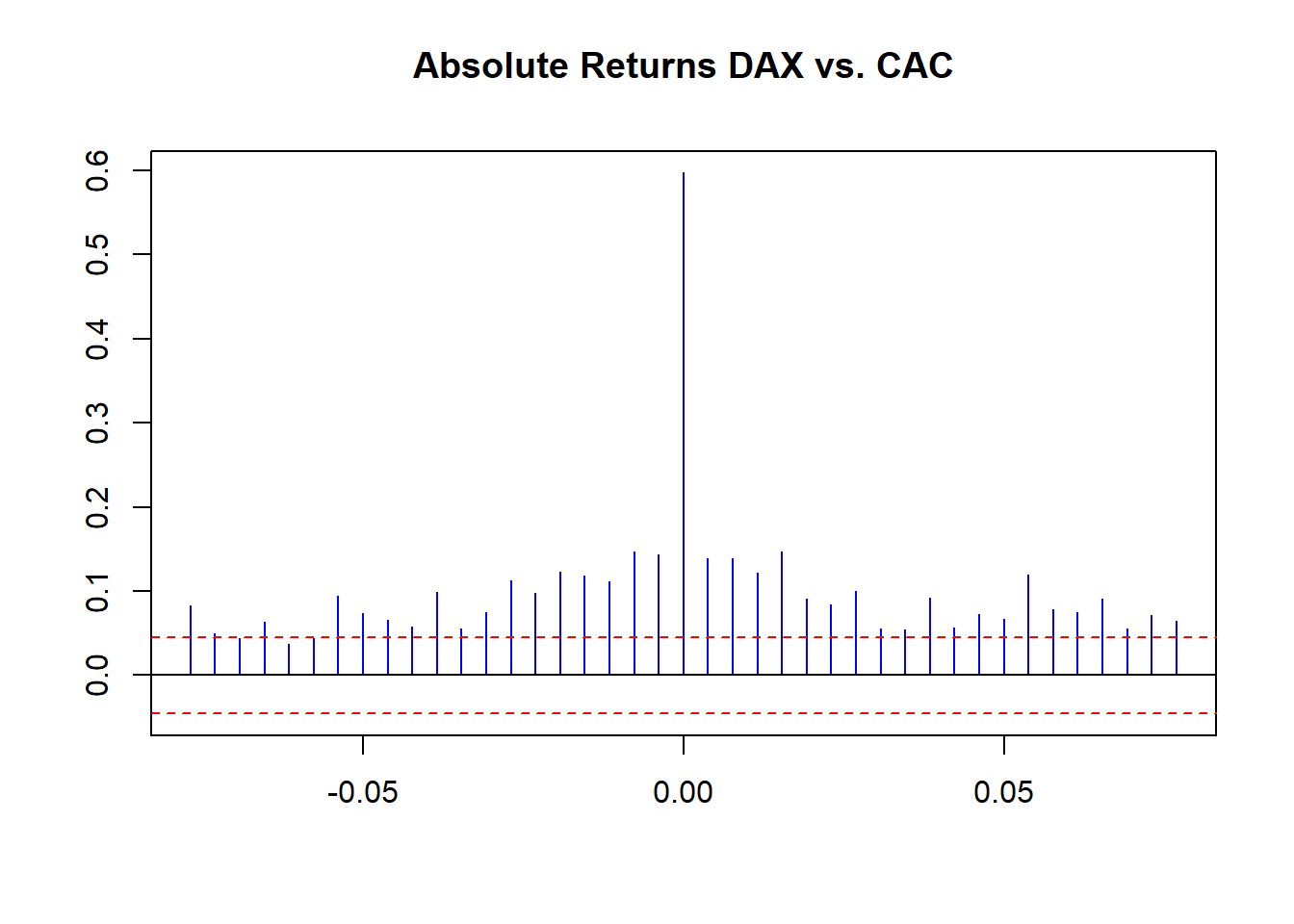
Kami melihat beberapa korelasi mentah kecil sepanjang waktu dengan pengembalian mentah. Lebih mengungkapkan, kita melihat volatilitas pengelompokan korelasi menggunakan ukuran kembali. Kita dapat melakukan satu percobaan lagi: korelasi bergulir menggunakan fungsi ini:
corr.rolling <- function (x) { dim <- ncol (x) corr.r <- cor (x)[ lower.tri ( diag (dim), diag = FALSE )] return (corr.r) } Kami kemudian menanamkan fungsi korelasi bergulir kami,
corr.rolling , ke dalam fungsi rollapply (lihat yang ini menggunakan ??rollapply di konsol). Pertanyaan yang perlu kita jawab adalah: Bagaimana sejarah korelasi, dan dari sejarah, pola korelasi di pasar saham Inggris dan UE? Jika ada "sejarah" dengan "pola," maka kita harus mengelola risiko bahwa melakukan bisnis di satu negara pasti akan mempengaruhi bisnis di negara lain. Implikasinya adalah bahwa hal-hal buruk akan diikuti oleh hal-hal buruk lebih sering daripada hal-hal baik. Implikasinya menambah implikasi serupa di seluruh pasar. corr.returns <- rollapply (EuStockMarkets.return, width = 250 , corr.rolling, align = "right" , by.column = FALSE ) colnames (corr.returns) <- c ( "DAX & CAC" , "DAX & SMI" , "DAX & FTSE" , "CAC & SMI" , "CAC & FTSE" , "SMI & FTSE" ) plot (corr.returns, xlab = "" , main = "" ) 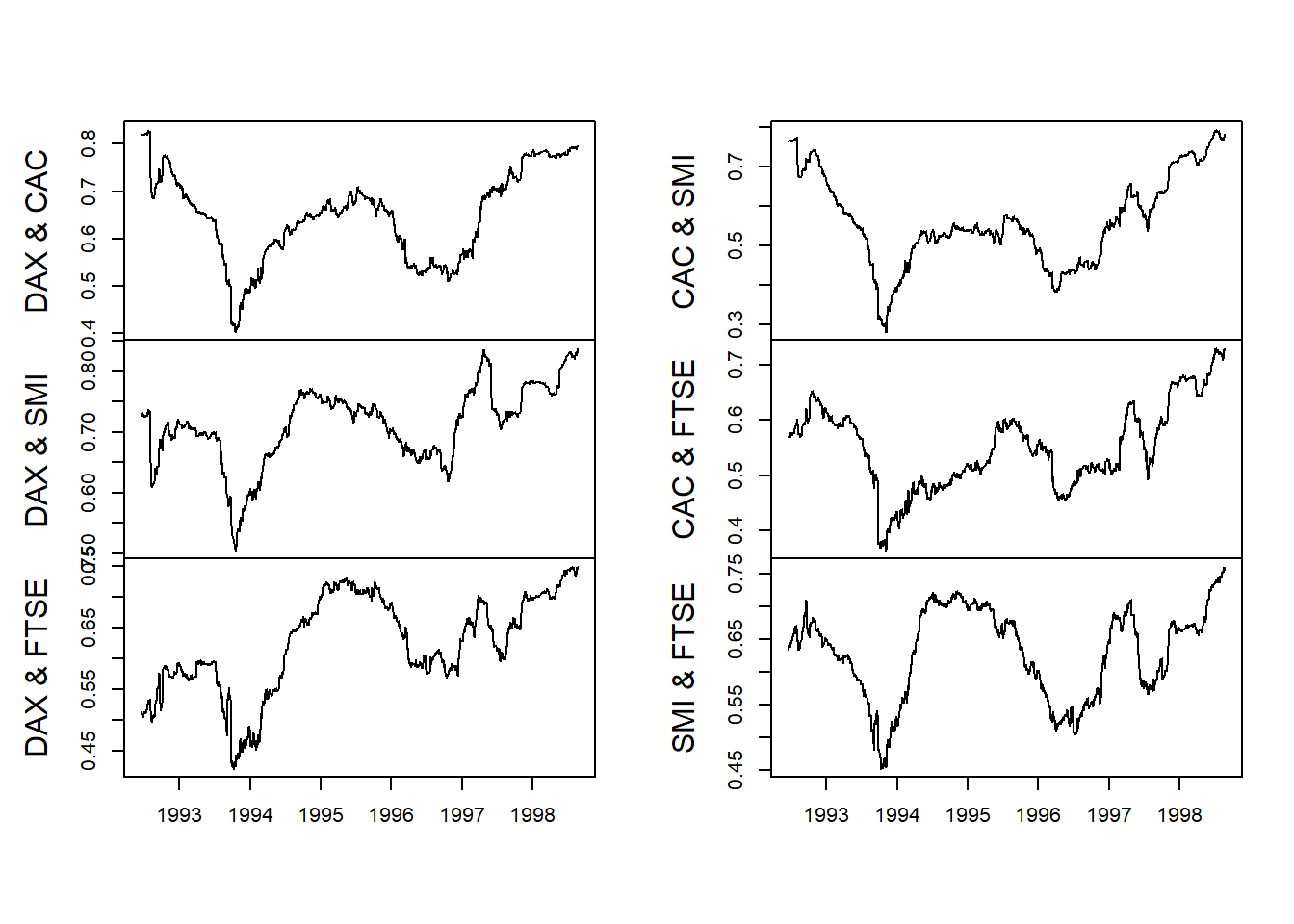
Sekali lagi kami mengamati pengelompokan volatilitas dari pengelompokan ukuran absolut pengembalian. Kinerja ekonomi tentu saja tunduk pada dinamika yang sama dengan yang kita lihat untuk variabel keuangan tunggal seperti Brent.
Mari kita ulang beberapa pekerjaan yang baru saja kita lakukan dengan menggunakan serangkaian teknik lain. Kali ini kami menggunakan transformasi "Fisher". Cari Fisher di Wikipedia dan dalam teks referensi Anda.
- Bagaimana Transformasi Fisher dapat membantu kita menjawab pertanyaan bisnis kita?
- Untuk tiga perusahaan Spanyol, Iberdrola, Endesa, dan Repsol, meniru eksperimen pasar saham Brent dan UE di atas dengan ukuran dan ekor absolut. Di sini kita sudah memiliki "seri" yang dibahas.
Pertama, transformasi Fisher adalah rutinitas smoothing yang membantu kita memilah-milah volitilitas suatu varian. Ini melakukan ini dengan menarik beberapa shockiness (yaitu, outlier dan suara menyimpang) dari deret waktu asli. Dalam frasa, ini membantu kita melihat hutan (atau kayu) untuk pepohonan.
Kami sekarang mereplikasi percobaan di bursa Brent dan UE.Kami kembali memuat beberapa paket dan mendapatkan beberapa data menggunakan
quantmod getSymbols dari bursa saham Madrid untuk mencocokkan contoh kerja awal kami dengan perusahaan Iberian. Kemudian hitung pengembalian dan bergabung menjadi file master. require (xts) require (qrmdata) require (quantreg) require (quantmod) require (matrixStats) tickers <- c ( "ELE.MC" , "IBE.MC" , "REP.MC" ) getSymbols (tickers) ## [1] "ELE.MC" "IBE.MC" "REP.MC" REP.r <- na.omit ( diff ( log (REP.MC[, 4 ]))[ - 1 ]) IBE.r <- na.omit ( diff ( log (IBE.MC[, 4 ]))[ - 1 ]) ELE.r <- na.omit ( diff ( log (ELE.MC[, 4 ]))[ - 1 ]) # clean up missing values ALL.r <- na.omit ( merge ( REP = REP.r, IBE = IBE.r, ELE = ELE.r, all = FALSE )) Selanjutnya kita plot pengembalian dan nilai absolutnya, ACF dan pacf, semua seperti yang kita lakukan di Brent. Sekali lagi kita lihat
- Kegigihan pengembalian
- Pentingnya ukuran kembali
- Pengelompokan volatilitas
plot (ALL.r) 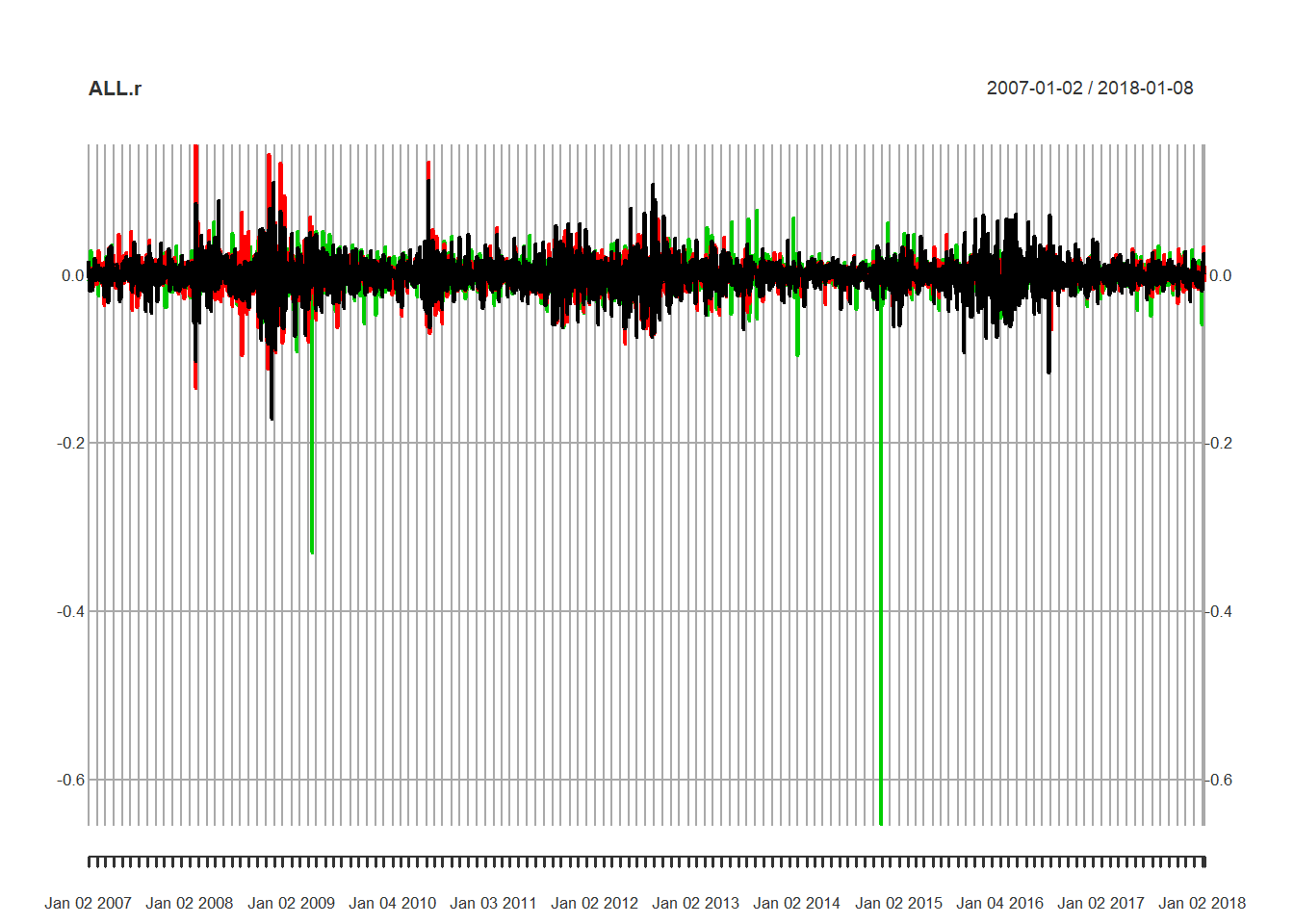
par ( mfrow = c ( 2 , 1 )) acf (ALL.r) 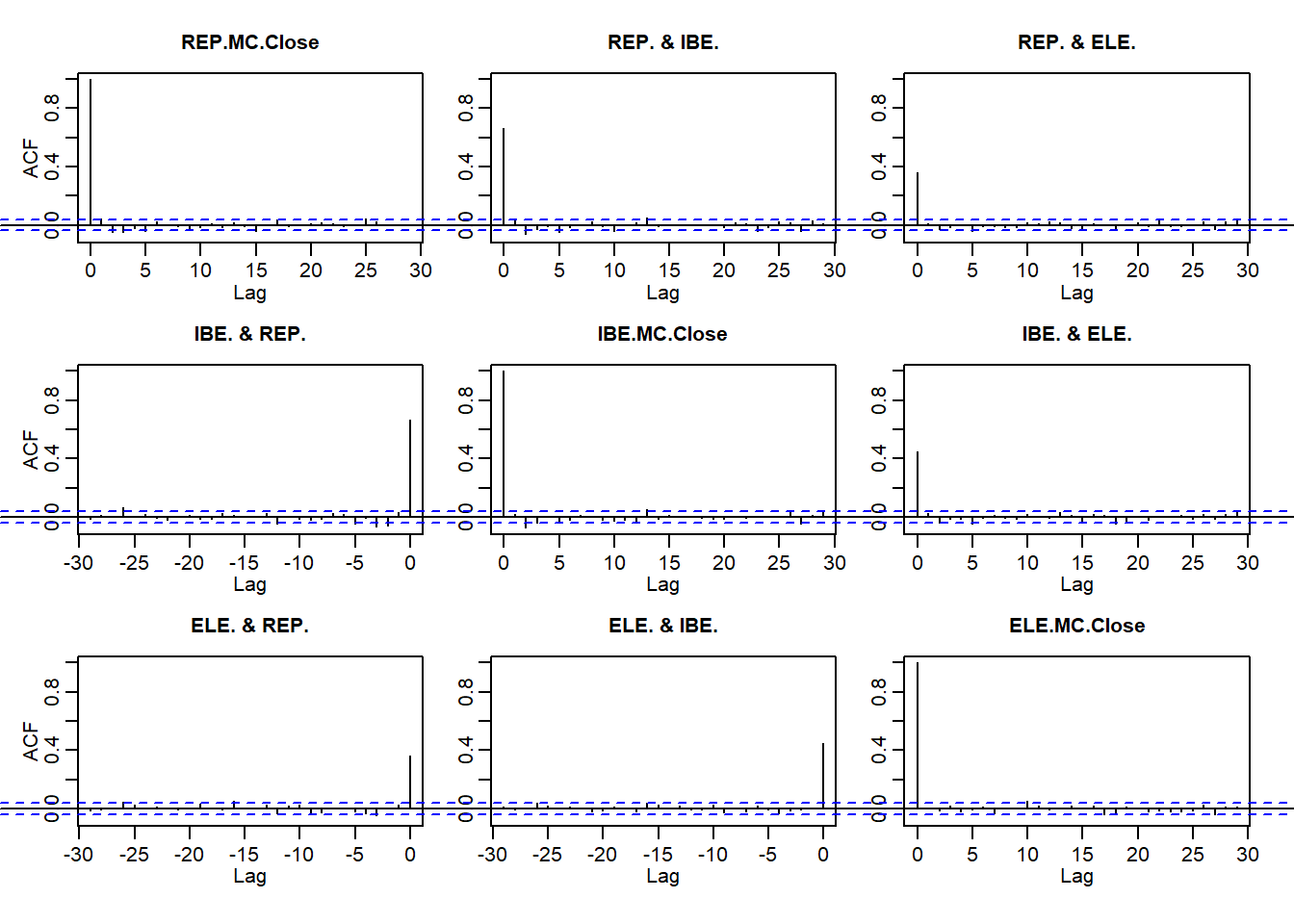
par ( mfrow = c ( 2 , 1 )) acf ( abs (ALL.r)) 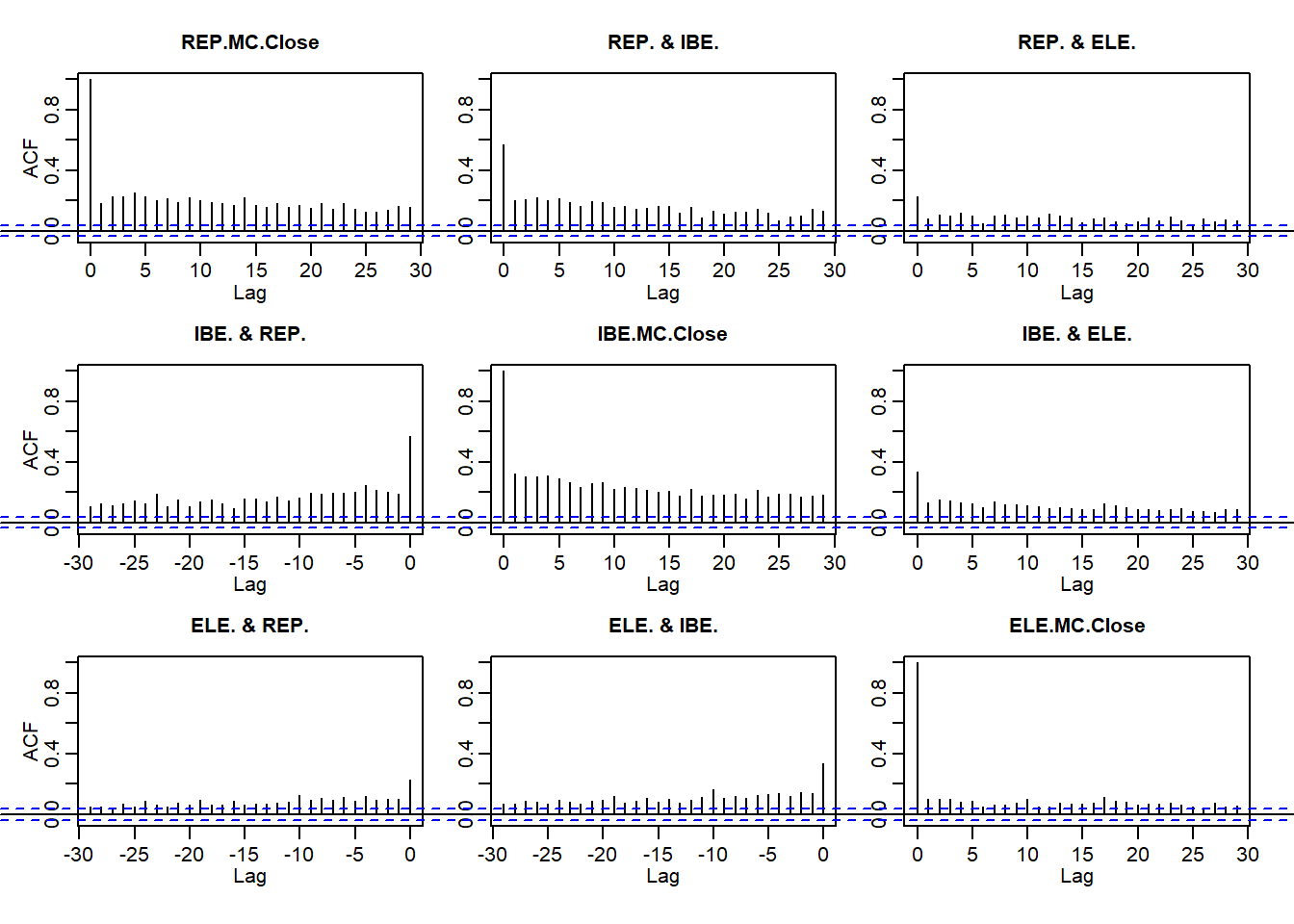
par ( mfrow = c ( 2 , 1 )) pacf (ALL.r) 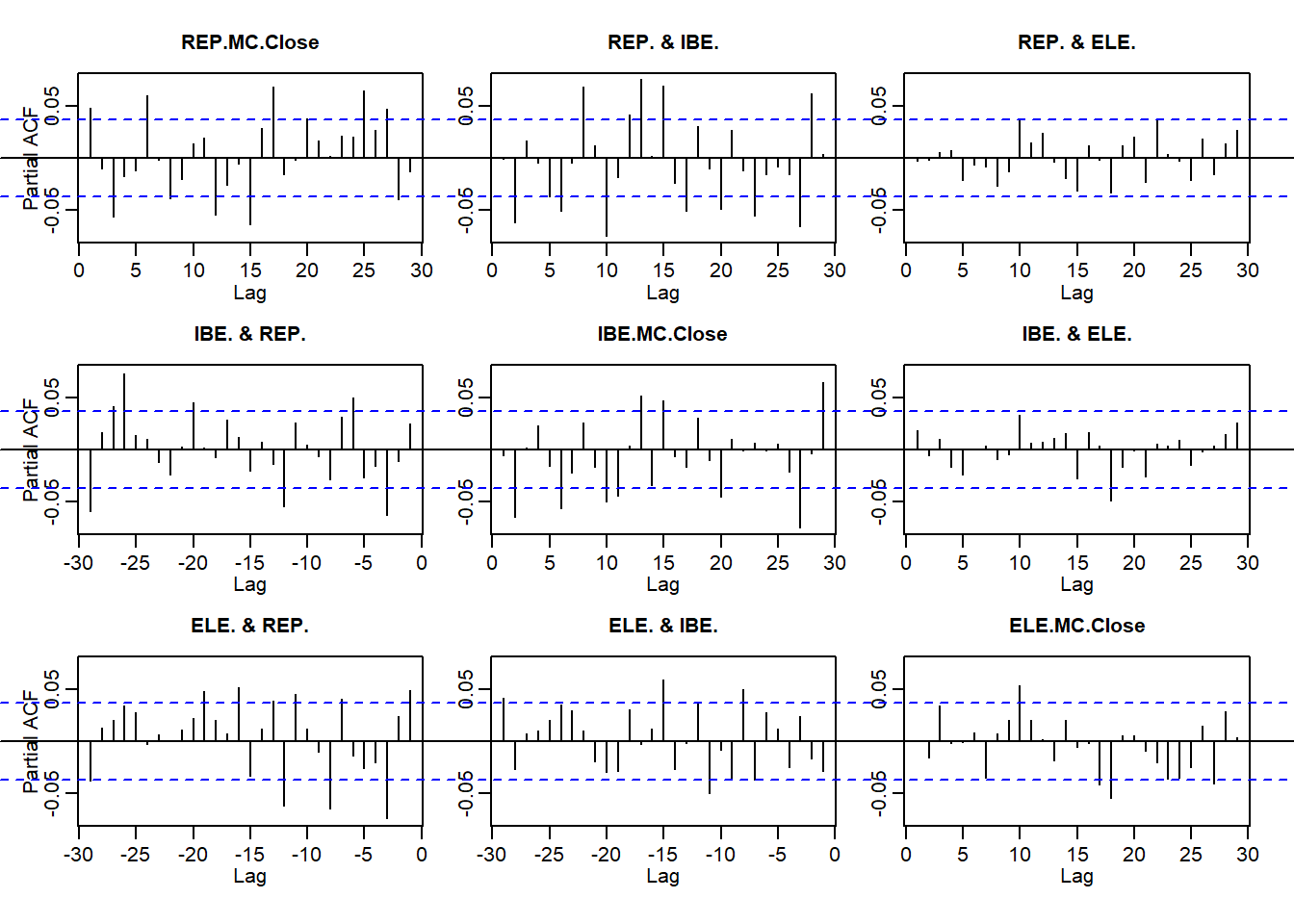
par ( mfrow = c ( 2 , 1 )) pacf ( abs (ALL.r)) 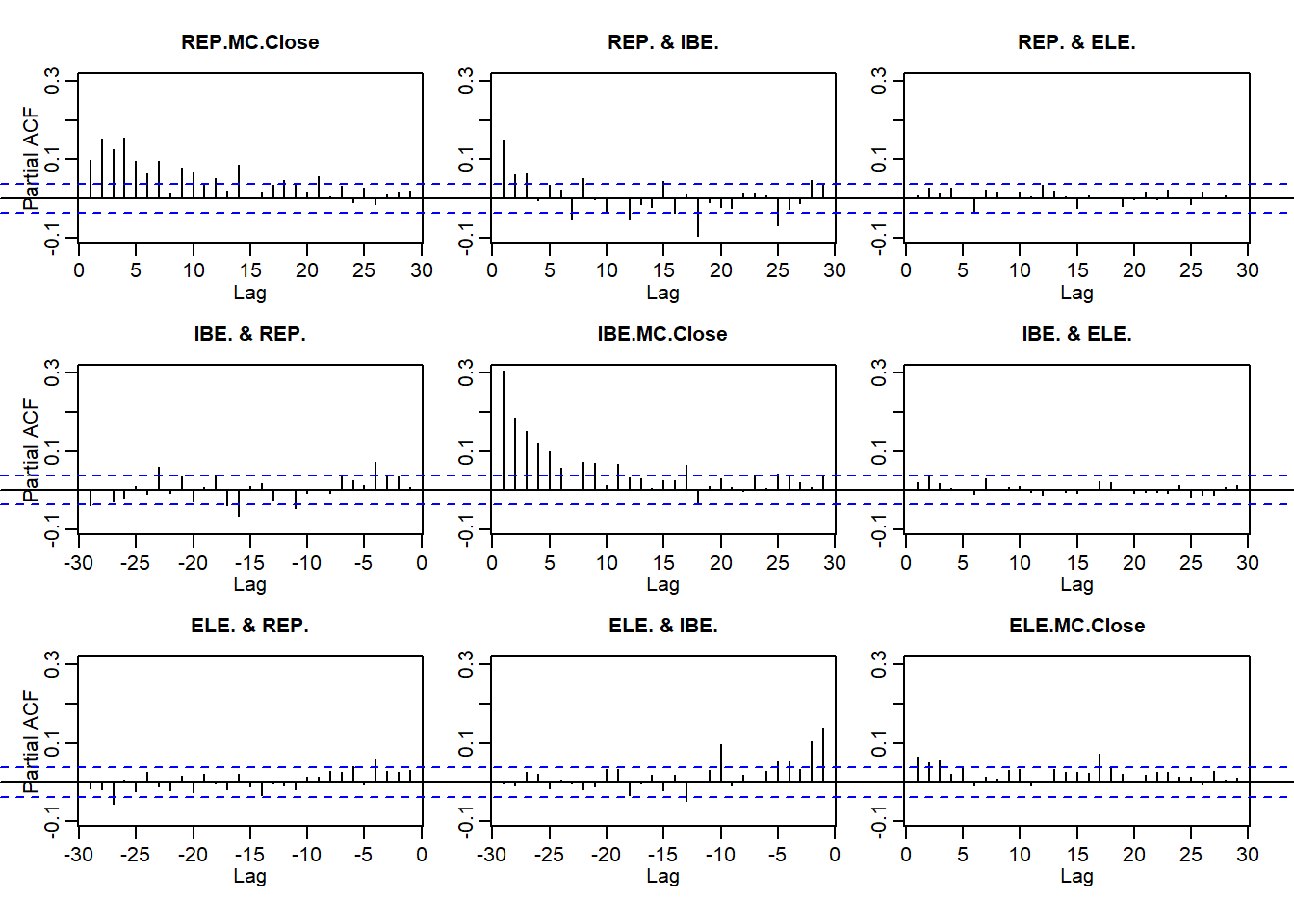
Mari kita periksa struktur korelasi pasar di mana kita dapat mengamati
- Hubungan antara korelasi dan volatilitas
- Bagaimana regresi kuantil membuat kita memahami episode stres tinggi (tinggi dan rendah)
R.corr <- apply.monthly (ALL.r, FUN = cor) R.vols <- apply.monthly (ALL.r, FUN = colSds) ## from MatrixStats head (R.corr, 3 ) ## [,1] [,2] [,3] [,4] [,5] [,6] ## 2007-01-31 1 0.3613554 -0.27540757 0.3613554 1 0.10413800 ## 2007-02-28 1 0.5661814 -0.09855544 0.5661814 1 0.10760477 ## 2007-03-30 1 0.4500982 -0.08874664 0.4500982 1 0.08538064 ## [,7] [,8] [,9] ## 2007-01-31 -0.27540757 0.10413800 1 ## 2007-02-28 -0.09855544 0.10760477 1 ## 2007-03-30 -0.08874664 0.08538064 1 head (R.vols, 3 ) ## REP.MC.Close IBE.MC.Close ELE.MC.Close ## 2007-01-31 0.009787963 0.007892759 0.009777426 ## 2007-02-28 0.009181099 0.014571945 0.007674848 ## 2007-03-30 0.015317331 0.012719792 0.010919155 R.corr. 1 <- matrix (R.corr[ 1 , ], nrow = 3 , ncol = 3 , byrow = FALSE ) rownames (R.corr. 1 ) <- tickers colnames (R.corr. 1 ) <- tickers head (R.corr. 1 ) ## ELE.MC IBE.MC REP.MC ## ELE.MC 1.0000000 0.3613554 -0.2754076 ## IBE.MC 0.3613554 1.0000000 0.1041380 ## REP.MC -0.2754076 0.1041380 1.0000000 R.corr <- R.corr[, c ( 2 , 3 , 6 )] colnames (R.corr) <- c ( "ELE.IBE" , "ELE.REP" , "IBE.REP" ) colnames (R.vols) <- c ( "ELE.vols" , "IBE.vols" , "REP.vols" ) head (R.corr, 3 ) ## ELE.IBE ELE.REP IBE.REP ## 2007-01-31 0.3613554 -0.27540757 0.10413800 ## 2007-02-28 0.5661814 -0.09855544 0.10760477 ## 2007-03-30 0.4500982 -0.08874664 0.08538064 head (R.vols, 3 ) ## ELE.vols IBE.vols REP.vols ## 2007-01-31 0.009787963 0.007892759 0.009777426 ## 2007-02-28 0.009181099 0.014571945 0.007674848 ## 2007-03-30 0.015317331 0.012719792 0.010919155 R.corr.vols <- merge (R.corr, R.vols) plot.zoo ( merge (R.corr.vols)) 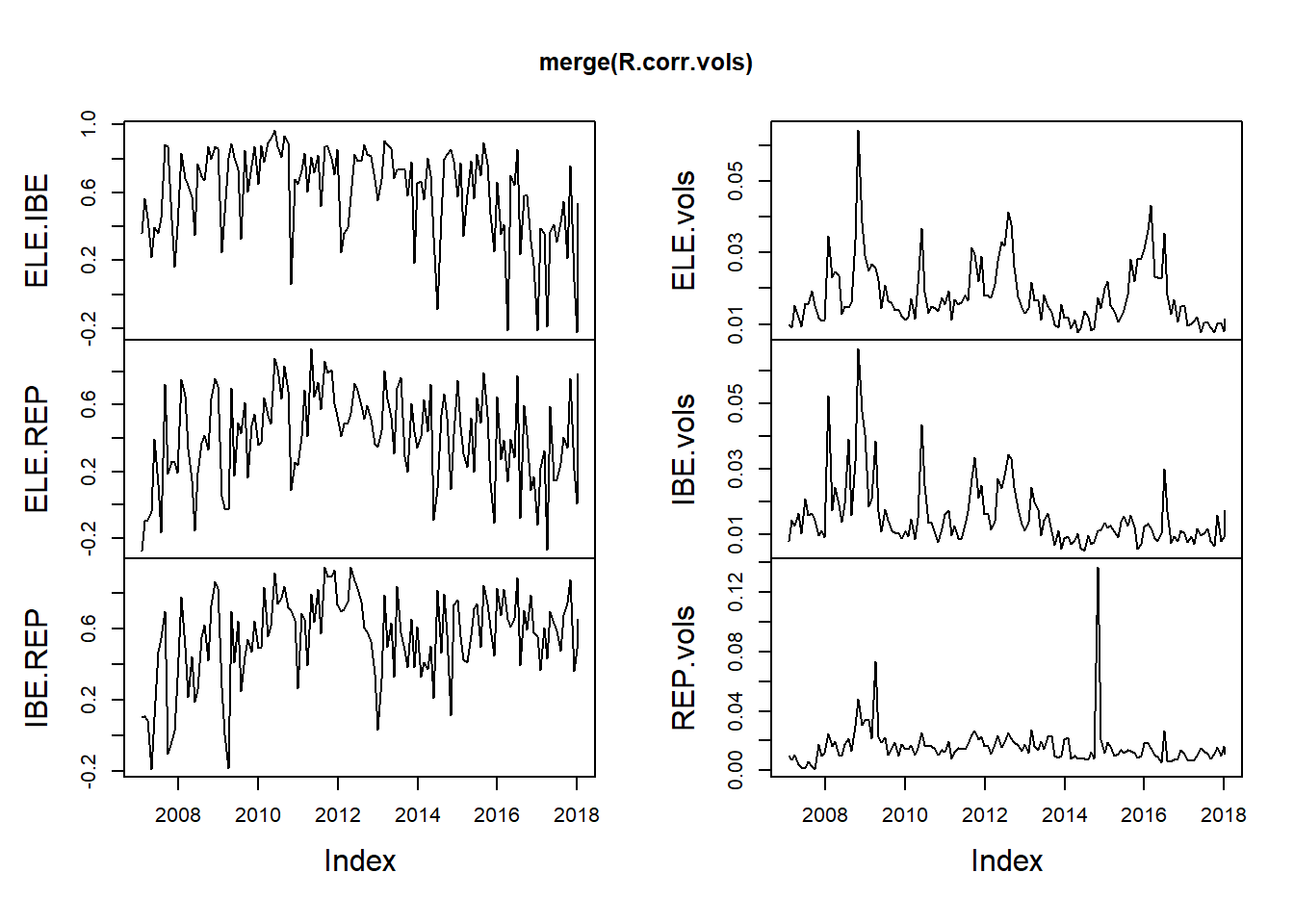
ELE.vols <- as.numeric (R.corr.vols[, "ELE.vols" ]) IBE.vols <- as.numeric (R.vols[, "IBE.vols" ]) REP.vols <- as.numeric (R.vols[, "REP.vols" ]) length (ELE.vols) ## [1] 133 fisher <- function (r) { 0.5 * log (( 1 + r) / ( 1 - r)) } rho.fisher <- matrix ( fisher ( as.numeric (R.corr.vols[, 1 : 3 ])), nrow = length (ELE.vols), ncol = 3 , byrow = FALSE ) 4.3.1 Aktif ke kuantil
Ini adalah bagian regresi kuantil dari paket. Regresi kuantitatif menemukan hubungan rata-rata antara variabel dependen dan independen seperti kuadrat terkecil biasa dengan satu pengecualian. Alih-alih memusatkan regresi pada rata-rata aritmatika dari variabel dependen, regresi kuantil memusatkan regresi pada kuantil tertentu dari variabel dependen. Jadi alih-alih menggunakan rata-rata aritemetik dari korelasi bergulir, kita sekarang menggunakan kuantil ke-10, atau median, yang merupakan kuantil ke-50 sebagai referensi kami. Ini sangat masuk akal karena kita telah menetapkan bahwa seri yang kita tangani di sini tebal, miring, dan tentu saja tidak terdistribusi secara normal.
Inilah cara kami menggunakan paket
quantreg .- Kami menetapkan
taussebagai jumlah yang menarik. - Kami menjalankan regresi kuantil menggunakan paket
quantregdan panggilan ke fungsirq. - Kita dapat melihat hasil regresi kuantil ke dalam regresi model linier standar.
- Kami dapat membuat kepekaan analisis kami dengan kisaran batas atas dan bawah pada estimasi parameter hubungan antara korelasi dan volatilitas. Analisis sensitivitas ini adalah interval kepercayaan yang didasarkan pada regresi kuantil.
require (quantreg) taus <- seq ( 0.05 , 0.95 , 0.05 ) fit.rq.ELE.IBE <- rq (rho.fisher[, 1 ] ~ ELE.vols, tau = taus) fit.lm.ELE.IBE <- lm (rho.fisher[, 1 ] ~ ELE.vols) plot ( summary (fit.rq.ELE.IBE), parm = "ELE.vols" ) 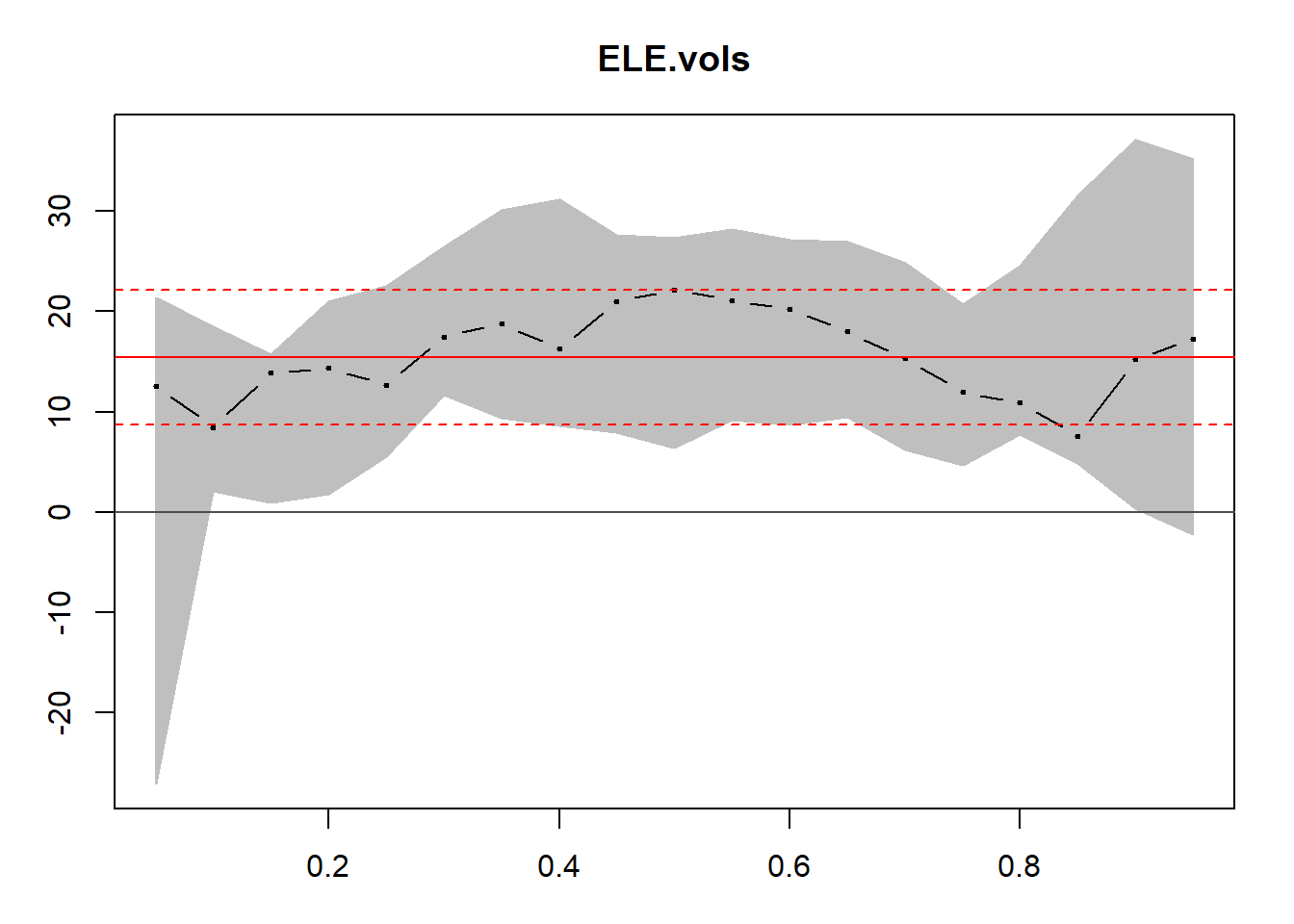
Di sini kami membuat estimasi dan memplot batas atas dan bawah.
taus1 <- c ( 0.05 , 0.95 ) ## fit the confidence interval (CI) plot (ELE.vols, rho.fisher[, 1 ], xlab = "ELE.vol" , ylab = "ELE.IBE" ) abline (fit.lm.ELE.IBE, col = "red" ) for (i in 1 : length (taus1)) { ## these lines will be the CI abline ( rq (rho.fisher[, 1 ] ~ ELE.vols, tau = taus1[i]), col = "blue" ) } grid () 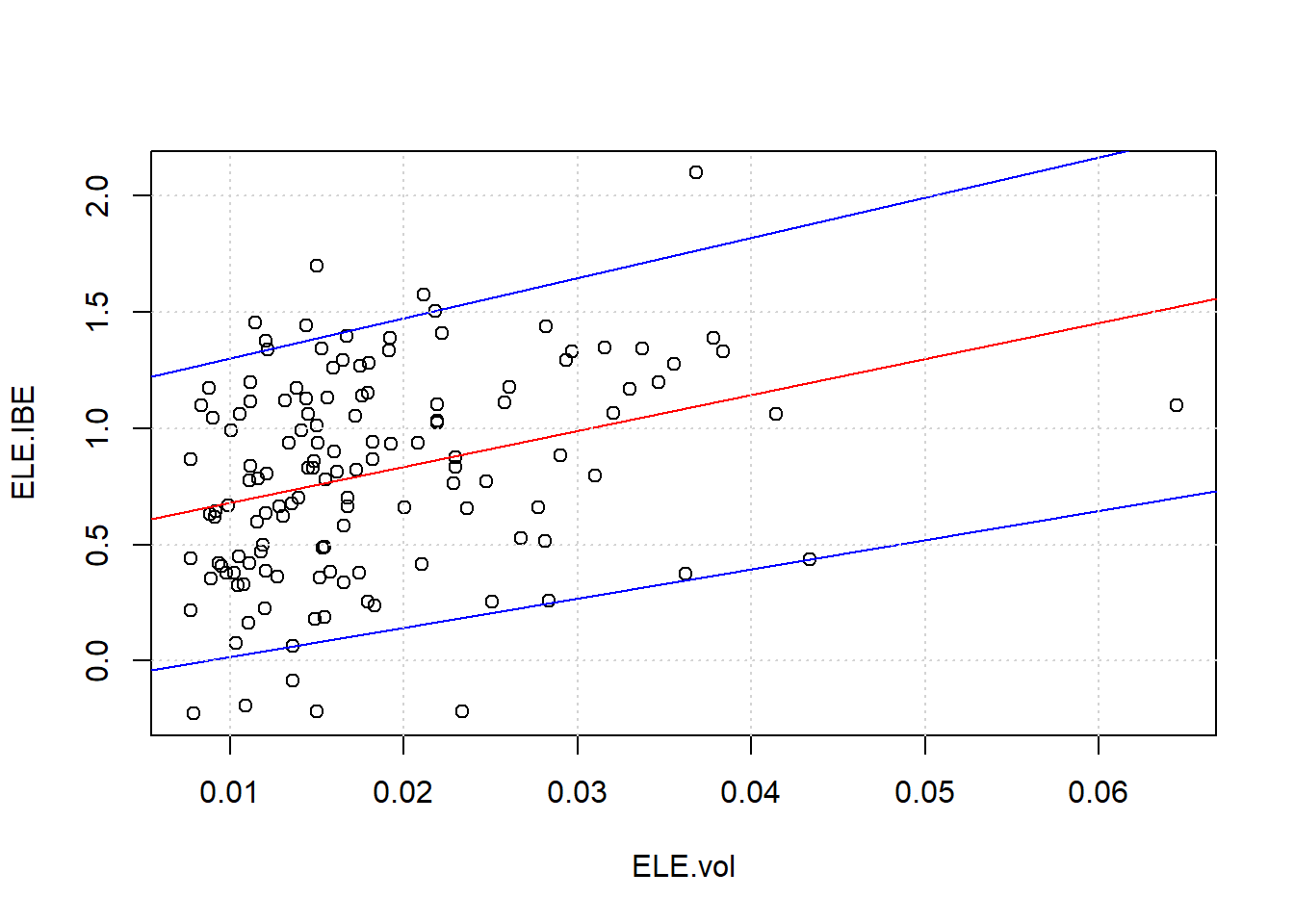
Regresi kuantitatif membantu kita melihat batas atas dan bawah. Hubungan antara periode stres tinggi dan korelasi berlimpah. Pasar-pasar ini hanya mencerminkan perilaku pembelian normal di berbagai jenis pertukaran: membeli makanan di Safeway atau Whole Foods, membeli jaminan untuk mengasuransikan proyek, menjual aset tidak likuid.
4.4 Waktu ada di pihak kita
Ke variabel penting lainnya, tingkat dan tingkat pertumbuhan Produk Nasional Bruto. Mari kita mulai dengan beberapa data Produk Nasional Bruto AS (GNP) dari situs web data terbuka St. Louis Fed ("FRED"). Kami mengakses https://fred.stlouisfed.org/series/GNPC96 untuk mengunduh GNP sungguhan dalam dolar 1996 berantai. Menyimpan ini sebagai file CSV kemudian membaca file yang disimpan ke ruang kerja
R kami. name <- "GNP" download <- read.csv ( "data/GNPC96.csv" ) Lihatlah datanya:
hist (download[, 2 ]) 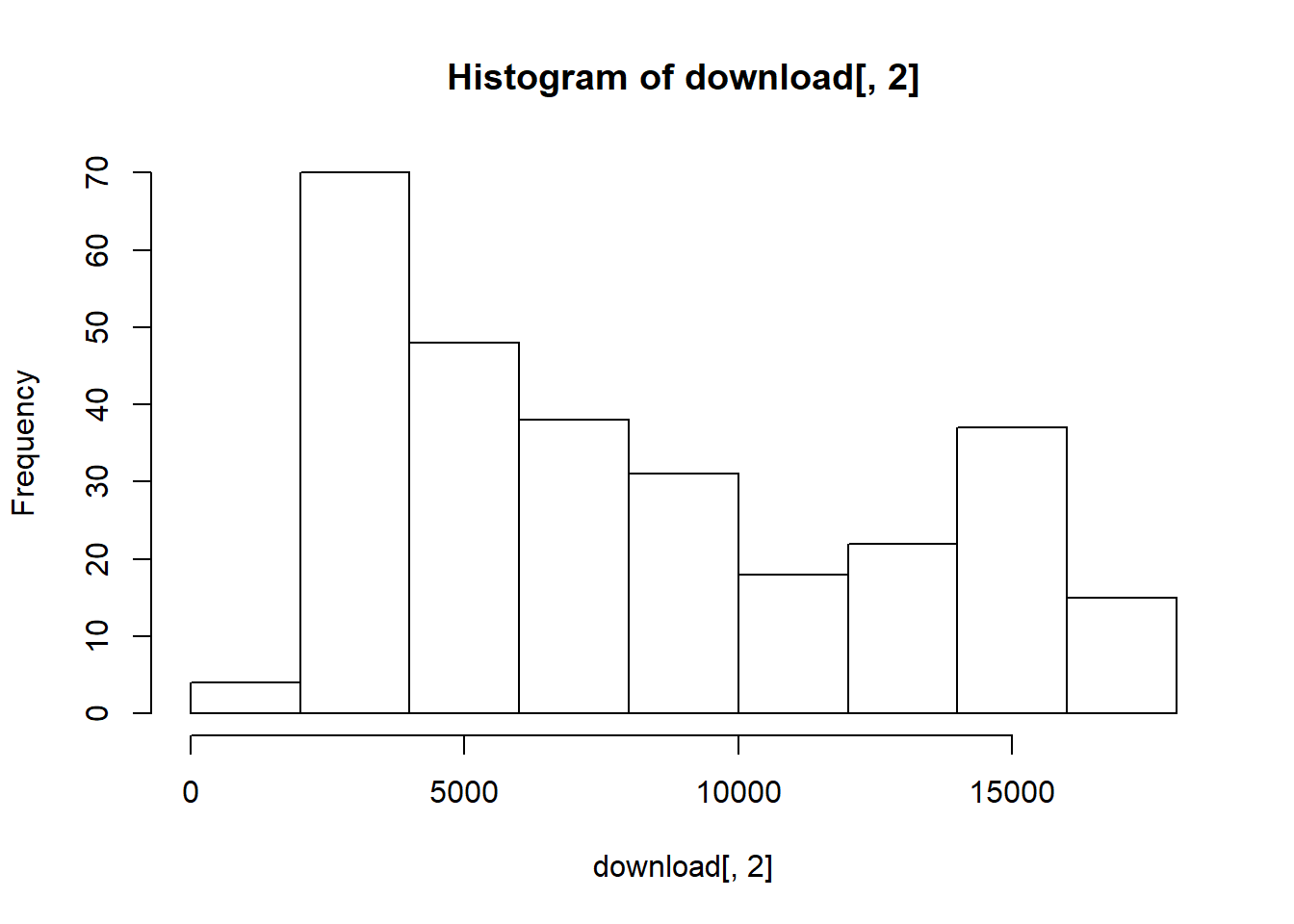
summary (download[, 2 ]) ## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 1943 3808 6659 8035 12385 17353 Kami kemudian membuat objek seri waktu mentah menggunakan fungsi
ts mana nama tanggal adalah tanggal, pilih beberapa data, dan menghitung tingkat pertumbuhan. Ini akan memungkinkan kami dan merencanakan fungsi untuk menggunakan tanggal untuk mengindeks data. Sekali lagi kami menggunakan perhitungan vektor diff(log(data)) . GNP <- ts (download[ 1 : 85 , 2 ], start = c ( 1995 , 1 ), freq = 4 ) GNP.rate <- 100 * diff ( log (GNP)) # In percentage terms str (GNP) ## Time-Series [1:85] from 1995 to 2016: 1947 1945 1943 1974 2004 ... head (GNP) ## [1] 1947.003 1945.311 1943.290 1974.312 2004.218 2037.215 head (GNP.rate) ## [1] -0.08694058 -0.10394485 1.58375702 1.50339765 1.63297193 0.55749065 Mari kita plot level dan nilai GNP serta komentar pada polanya.
plot (GNP, type = "l" , main = "US GNP Level" ) 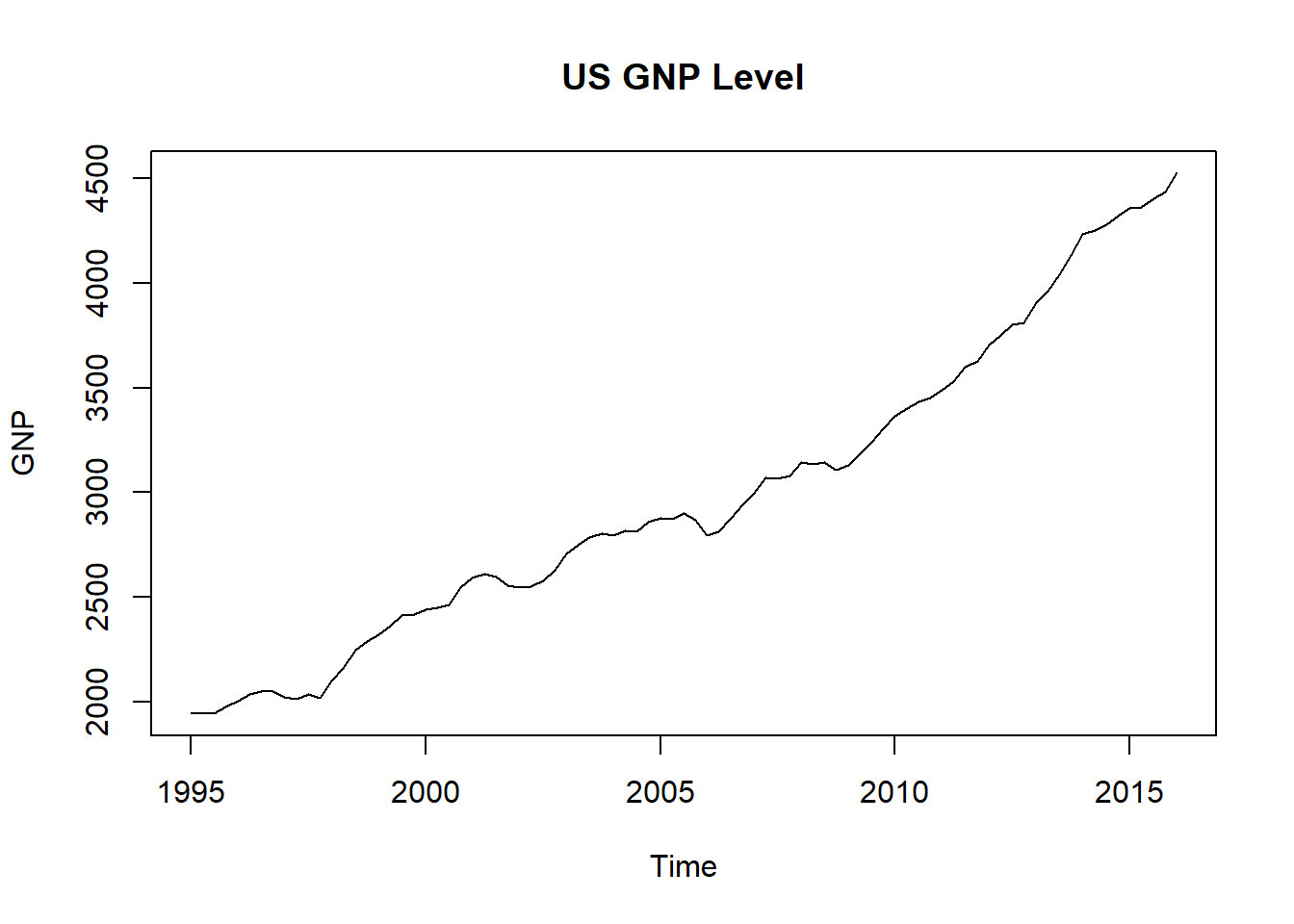
plot (GNP.rate, type = "h" , main = "GNP quarterly growth rates" ) abline ( h = 0 , col = "darkgray" ) 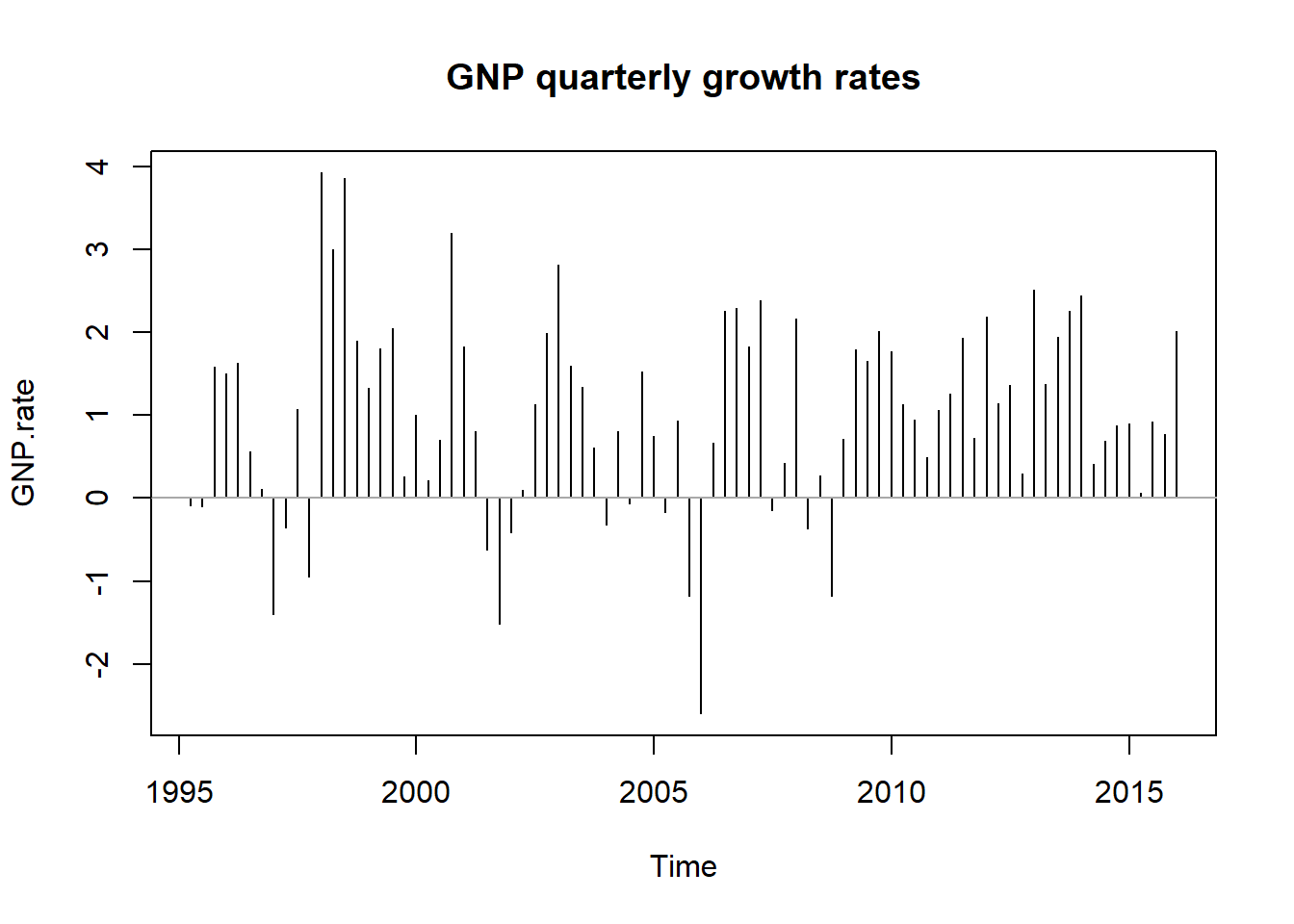
Kami melihat sebuah fenomena yang disebut "nonstasioneritas." Distribusi probabilitas (think
hist() ) tampaknya akan berubah seiring waktu (banyak versi hist() ). Ini berarti bahwa deviasi standar dan perubahan rata-rata juga (dan momen yang lebih tinggi seperti skewness dan kurtosis). Ada tren di tingkat ini dan tingkat sinusoidal yang berkurang. Singkatnya kami mengamati beberapa distribusi dicampur bersama dalam seri ini. Ini akan terjadi lagi dalam struktur suku bunga di mana kita akan menggunakan splines dan simpulnya untuk mengukur parameter berbagai distribusi yang bersembunyi tepat di bawah pasang surut dan aliran data.4.4.1 Memprakirakan GNP
Seperti biasa, mari kita lihat ACF dan PACF:
par ( mfrow = c ( 2 , 1 )) ##stacked up and down acf (GNP.rate) acf ( abs (GNP.rate)) 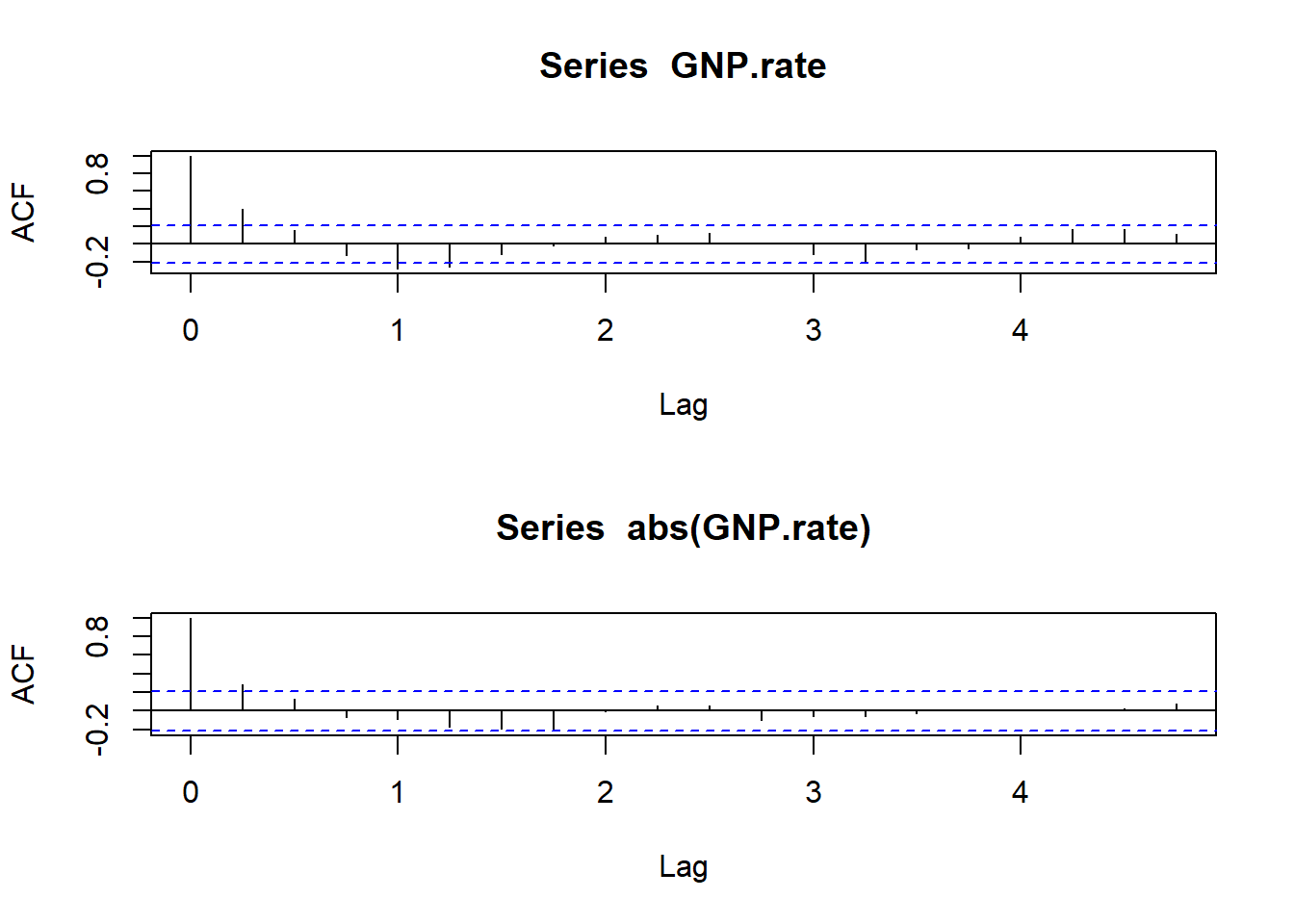
par ( mfrow = c ( 1 , 1 )) ##default setting Menurut kami apa yang sedang terjadi? Ada beberapa autokorelasi yang signifikan dalam 4 kuartal terakhir.Autokorelasi parsial juga menunjukkan beberapa kemungkinan hubungan 8 kuartal kembali.
Mari kita gunakan
arima estimasi waktu dan alat prediksi seri R Di dunia ini kami pikir ada regresi yang terlihat seperti ini:\ [x_t = a_0 + a_1 x_ {t-1} ... a_p x_ {tp} + b_1 \ varepsilon_ {t-1} + ... + b_q \ varepsilon_ {tq} \]
di mana \ (x_t \) adalah tingkat variabel pertama, \ (d = 1 \) , di sini GNP. Ada \ (p \) kelambatan dari kurs itu sendiri dan \ (q \) dari residual. Kami secara resmi menyebut ini proses pesanan Rata-rata Bergerak Autoregresif Terintegrasi \ ((p, d, q) \) , atau
ARIMA(p,d,q) singkatnya.Estimasi cepat dan mudah.
fit.rate <- arima (GNP.rate, order = c ( 2 , 1 , 1 )) Urutannya adalah 2 lag tarif, 1 perbedaan lebih lanjut (sudah dibedakan satu kali ketika kami menghitung
diff(log(GNP))), dan 1 lag residual. Mari mendiagnosis hasilnya dengan tsdiag() . Apa hasilnya? fit.rate ## ## Call: ## arima(x = GNP.rate, order = c(2, 1, 1)) ## ## Coefficients: ## ar1 ar2 ma1 ## 0.4062 0.0170 -1.000 ## se 0.1106 0.1107 0.038 ## ## sigma^2 estimated as 1.182: log likelihood = -126.49, aic = 260.98 Mari kita ambil istilah rata-rata bergerak dan bandingkan:
fit.rate. 2 <- arima (GNP.rate, order = c ( 2 , 0 , 0 )) fit.rate. 2 ## ## Call: ## arima(x = GNP.rate, order = c(2, 0, 0)) ## ## Coefficients: ## ar1 ar2 intercept ## 0.3939 0.0049 1.0039 ## se 0.1092 0.1093 0.1946 ## ## sigma^2 estimated as 1.168: log likelihood = -125.8, aic = 259.59 Kami memeriksa residu selanjutnya.
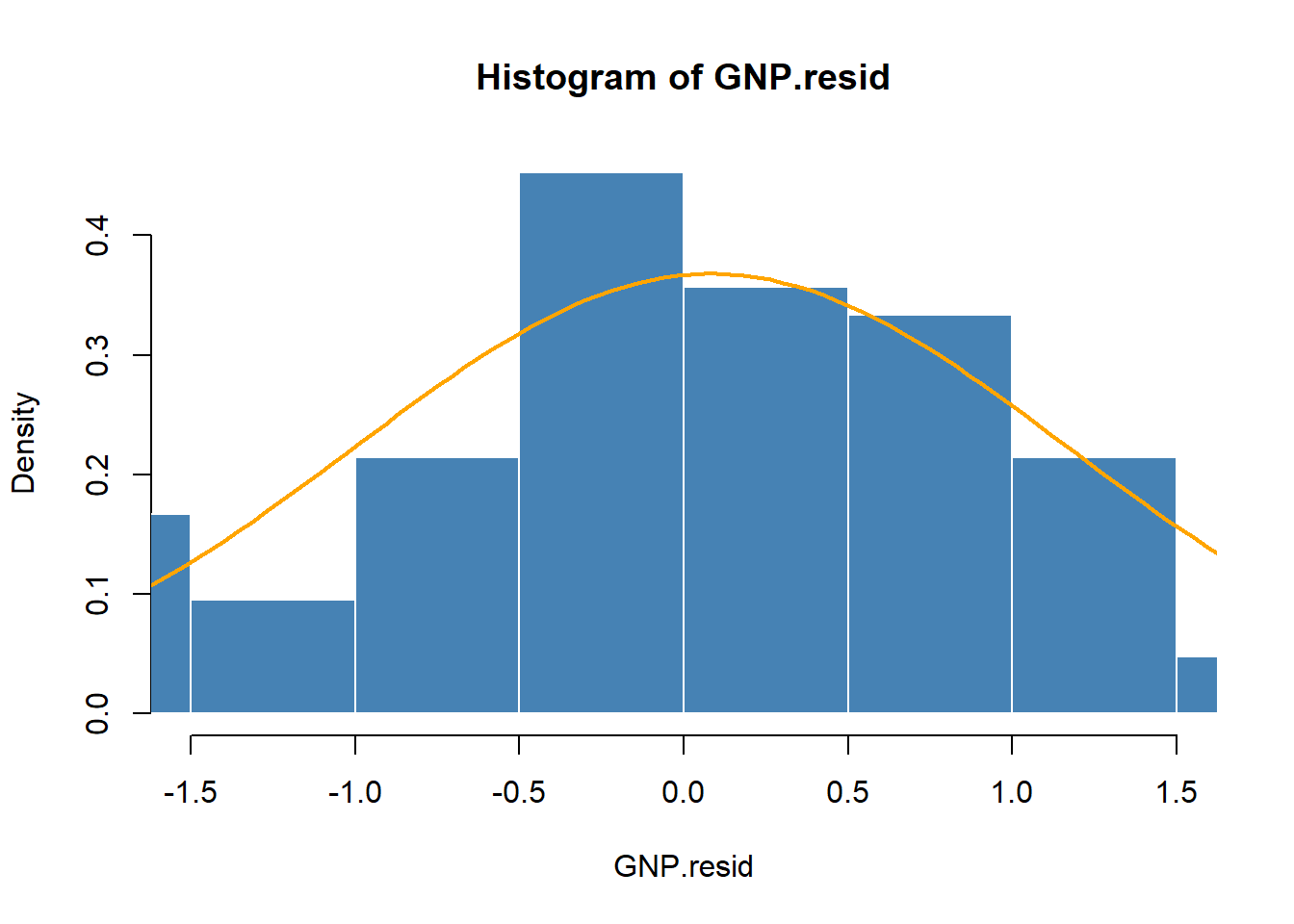
Fungsi
qqnorm kuantil aktual terhadap distribusi normal teoretis dari kuantil. Sebuah garis melalui scatterplot akan mengungkapkan penyimpangan dari kuantil aktual dari yang normal. Penyimpangan tersebut adalah kunci untuk memahami perilaku ekor, dan dengan demikian pengaruh potensial pencilan, pada pemahaman kita tentang data. qqnorm (GNP.resid) qqline (GNP.resid) 
Beberapa cara untuk menafsirkan bagan qq meliputi
- Garis diagonal adalah garis kuantil distribusi normal.
- Penyimpangan dari kuantil aktual dari garis kuantil normal berarti tidak normal.
- Terutama penyimpangan di salah satu (atau keduanya) ujung garis, mengeja ekor tebal dan lebih banyak "bentuk" daripada distribusi normal memungkinkan.
4.4.2 Residual lagi
Bagaimana kita bisa mulai mendiagnosis residu GNP? Mari kita gunakan paket ACF dan
moments untuk menghitung skewness dan kurtosis . Kami menemukan bahwa seri ini sangat berekor tebal dan berkorelasi seri sebagaimana dibuktikan oleh tersangka statistik yang biasa. Tapi tidak ada pengelompokan volatilitas. acf (GNP.resid) 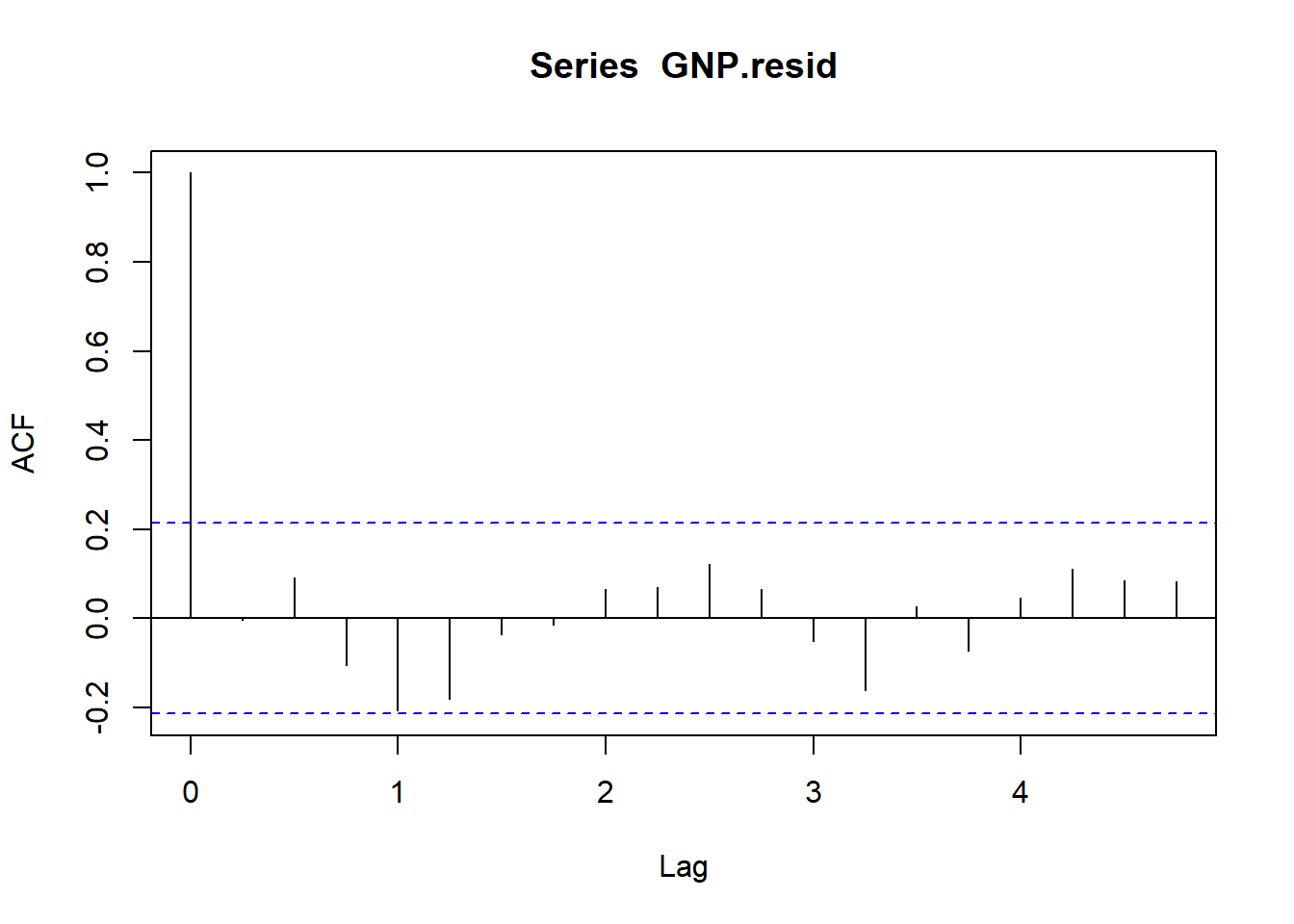
Sekarang mari kita lihat nilai absolut pertumbuhan (yaitu, ukuran pertumbuhan GNP). Ini akan membantu kita memahami aspek rangkaian waktu dari volatilitas residu GNP.
acf ( abs (GNP.resid)) 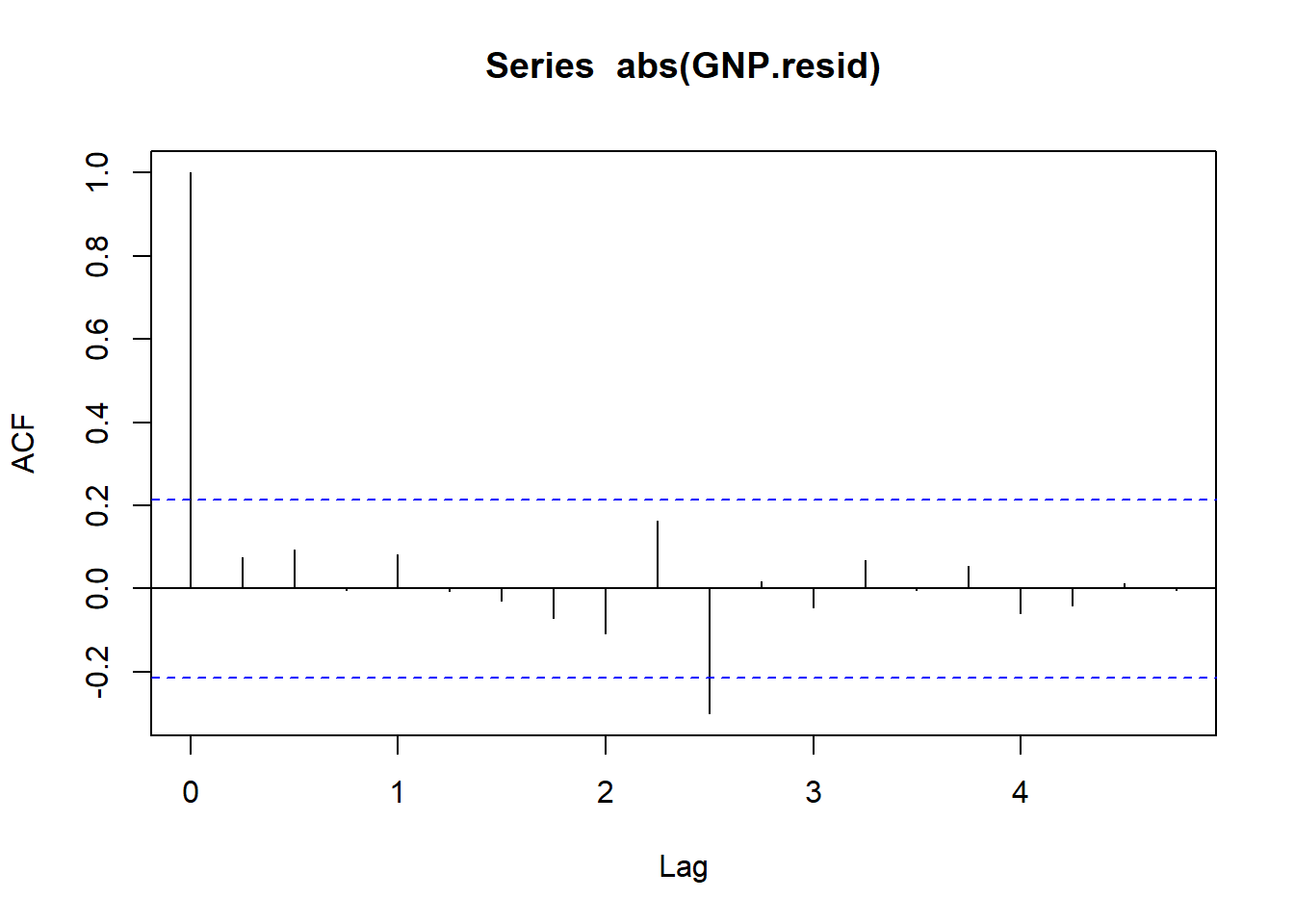
... dan menghitung statistik ekor.
require (moments) skewness (GNP.resid) ## [1] 0.2283692 ## attr(,"method") ## [1] "moment" kurtosis (GNP.resid) ## [1] 1.037626 ## attr(,"method") ## [1] "excess" Residu cenderung miring positif dan tidak terlalu tebal, karena distribusi normal memiliki definisi kurtosis sama dengan
3.00 . Oleh: Di mana ramalannya? (GNP.pred <- predict (fit.rate, n.ahead = 8 )) ## $pred ## Qtr1 Qtr2 Qtr3 Qtr4 ## 2016 1.410045 1.185815 1.084467 ## 2017 1.039485 1.019489 1.010602 1.006652 ## 2018 1.004896 ## ## $se ## Qtr1 Qtr2 Qtr3 Qtr4 ## 2016 1.093704 1.185259 1.204803 ## 2017 1.209512 1.210836 1.211272 1.211437 ## 2018 1.211504 Sekarang untuk sesuatu yang sangat menarik, render lain dari Hipotesis Pasar Efisien yang terkenal.
4.5 Berikan Bootnya
Tujuan kami adalah untuk menyimpulkan pentingnya hubungan statistik di antara para varian. Namun, kami tidak memiliki akses ke, atau "formula" tidak ada, yang memungkinkan kami untuk menghitung standar deviasi sampel dari estimator rata-rata.
- Konteksnya seberapa tergantungkah return saham hari ini pada hari kemarin?
- Kami ingin menggunakan distribusi data pengembalian dunia nyata, tanpa perlu asumsi tentang normalitas.
- Hipotesis nol \ (H_0 \) adalah kurangnya ketergantungan (yaitu, pasar yang efisien). Hipotesis alternatif \ (H_1 \)adalah bahwa pengembalian hari ini bergantung pada pengembalian yang lalu, rata-rata.
Strategi kami adalah mengubah data berulang kali, dan memperkirakan kembali suatu hubungan. Data diambil sampelnya menggunakan fungsi
replicate , dan sampel ACF dihitung. Ini memberi kita distribusi koefisien ACF di bawah hipotesis nol, \ (H0 \) : independensi, sambil menggunakan distribusi empiris dari data pengembalian.Mari kita gunakan pengembalian Repsol dan tarik autokorelasi pertama dari sampel dengan kode sederhana ini,
acf (REP.r, 1 ) 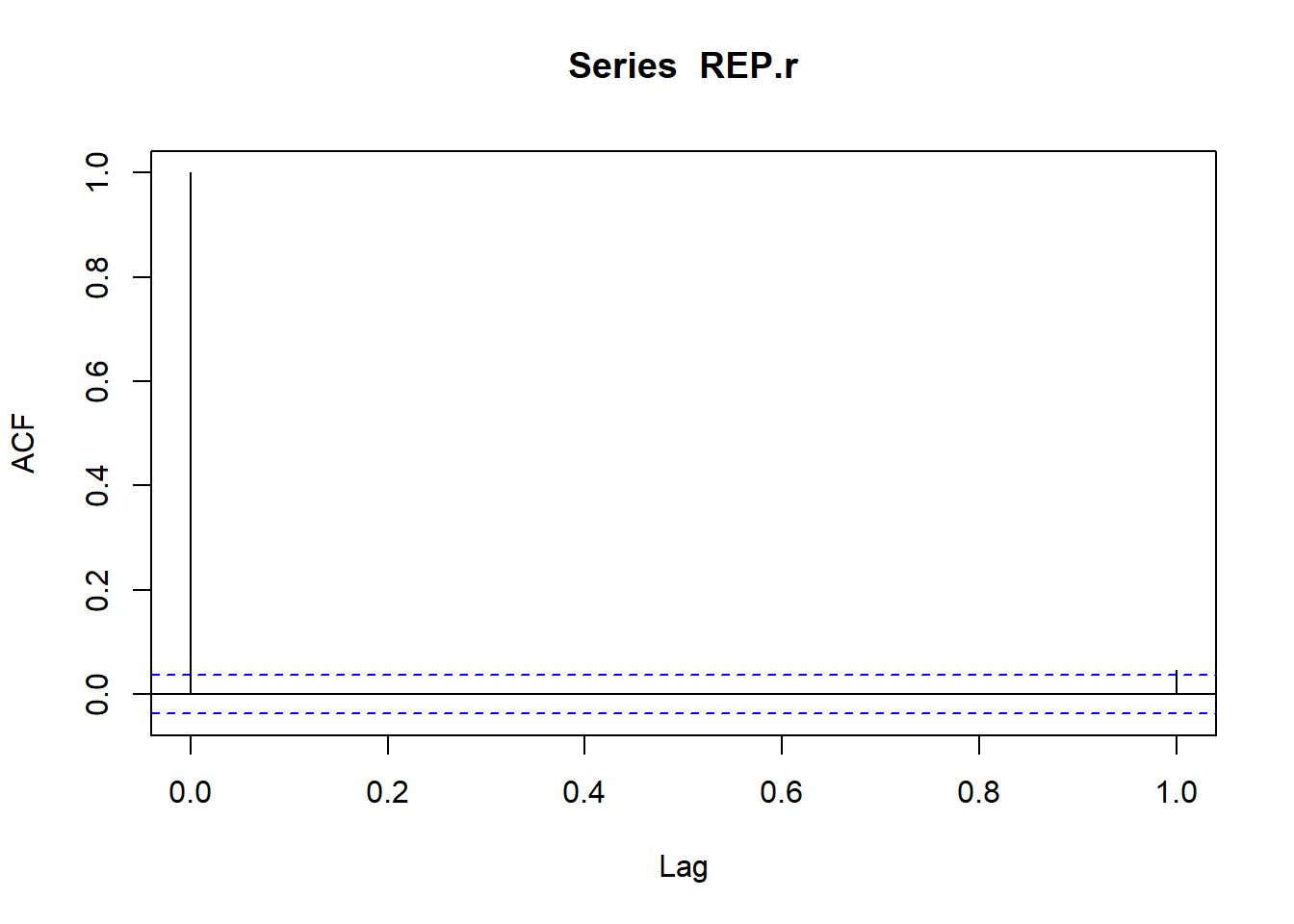
Tidak banyak yang bisa kita lihat, hanya blip, tetapi ada korelasi di atas garis 95%. Mari kita coba ide ini lebih lanjut.
- Kami memperoleh 2.500 penarikan dari distribusi autokorelasi pertama menggunakan fungsi
replicate. - Kami beroperasi di bawah hipotesis nol independensi, dengan asumsi pasar rasional (yaitu, pasar rasional adalah "hipotesis yang dipertahankan").
set.seed ( 1016 ) acf.coeff.sim <- replicate ( 2500 , acf ( sample (REP.r, size = 2500 , replace = FALSE ), lag = 2 , plot = FALSE ) $ acf[ 2 ]) summary (acf.coeff.sim) ## Min. 1st Qu. Median Mean 3rd Qu. Max. ## -0.01496 0.02576 0.03610 0.03617 0.04649 0.09576 Berikut adalah sebidang distribusi sarana sampel korelasi satu lag antara pengembalian berturut-turut.
hist (acf.coeff.sim, probability = TRUE , breaks = "FD" , xlim = c ( 0.04 , 0.05 ), col = "steelblue" , border = "white" ) 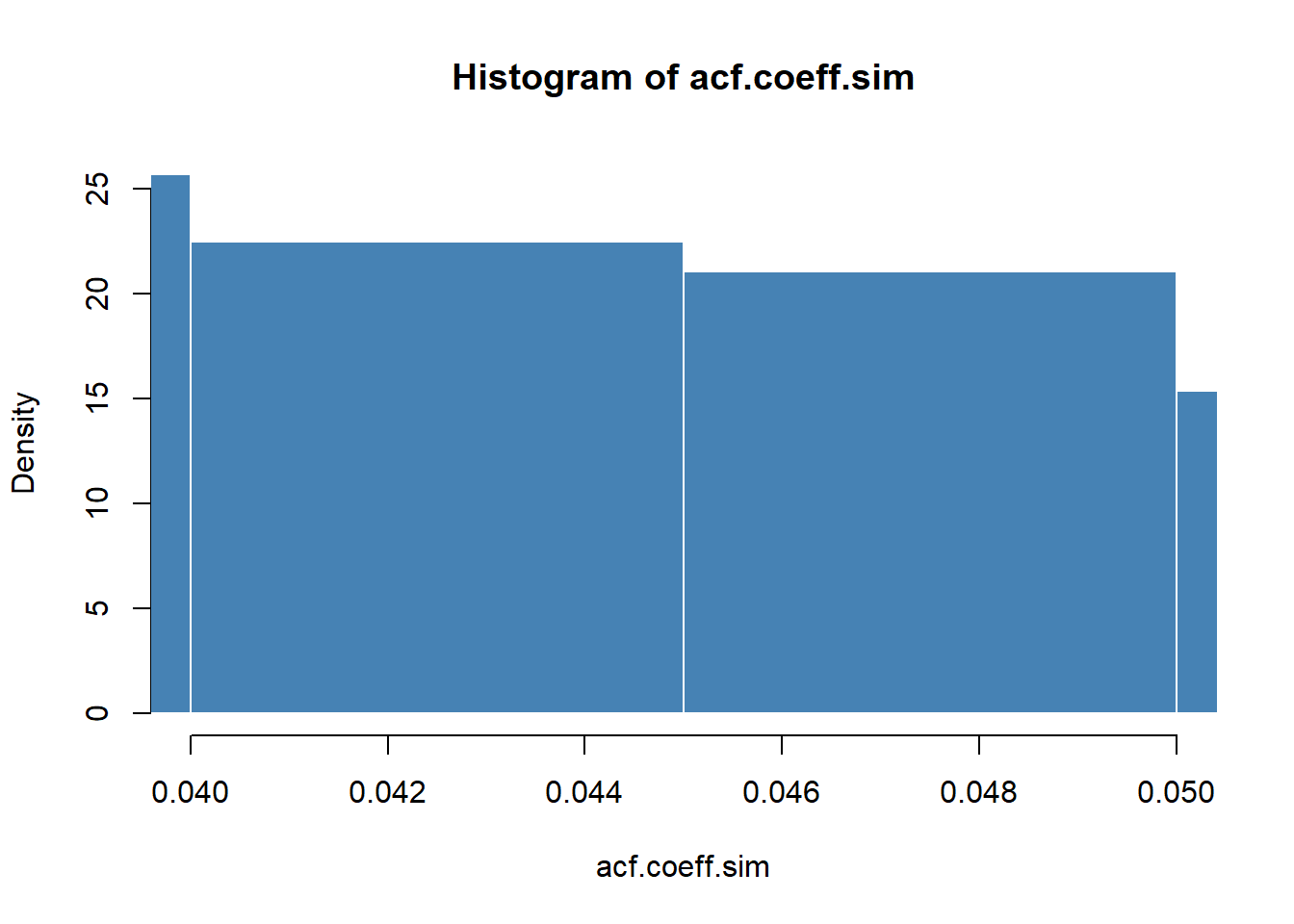
4.5.1 Cobalah latihan ini
Kami akan menyelidiki toleransi \ (5 \% \) dan \ (1 \% \) dari kedua ujung distribusi koefisien ACF 1-lag menggunakan pernyataan ini. Itu tadi suap! Ketika kita memikirkan inferensi, pertama-tama kita mengidentifikasi parameter minat, dan penaksirnya. Parameter itu adalah koefisien korelasi antara pengembalian saat ini dan kelambatan 1-periode. Kami memperkirakan parameter ini menggunakan riwayat pengembalian. Jika parameternya signifikan, dan mungkin, tidak sama dengan nol, maka kita akan memiliki alasan untuk percaya ada "pola" dalam "sejarah".
## At 95% tolerance level quantile (acf.coeff.sim, probs = c ( 0.025 , 0.975 )) ## 2.5% 97.5% ## 0.006069169 0.066687720 ## At 99% tolerance level quantile (acf.coeff.sim, probs = c ( 0.005 , 0.995 )) ## 0.5% 99.5% ## -0.004529213 0.075026818 ## And the (t.sim <- mean (acf.coeff.sim) / sd (acf.coeff.sim)) ## [1] 2.383801 ( 1 - pt (t.sim, df = 2 )) ## [1] 0.06998016 Berikut adalah beberapa jawaban yang sangat sementara dan sementara untuk direnungkan.
- Nilai kuantitas sangat sempit ...
- Seberapa sempit (merasa seperti menolak hipotesis nol)?
- Stat-itu besar, tapi ...
- ... tidak ada tapi !, probabilitas bahwa kita akan salah untuk menolak hipotesis nol sangat kecil.
Di sini kami memplot kerapatan simulasi dan kuantil atas dan bawah, bersama dengan estimasi koefisien lag-1:
plot ( density (acf.coeff.sim), col = "blue" ) abline ( v = 0 ) abline ( v = quantile (acf.coeff.sim, probs = c ( 0.025 , 0.975 )), lwd = 2 , col = "red" ) abline ( v = acf (REP.r, 1 , plot = FALSE ) $ acf[ 2 ], lty = 2 , lwd = 4 , col = "orange" ) 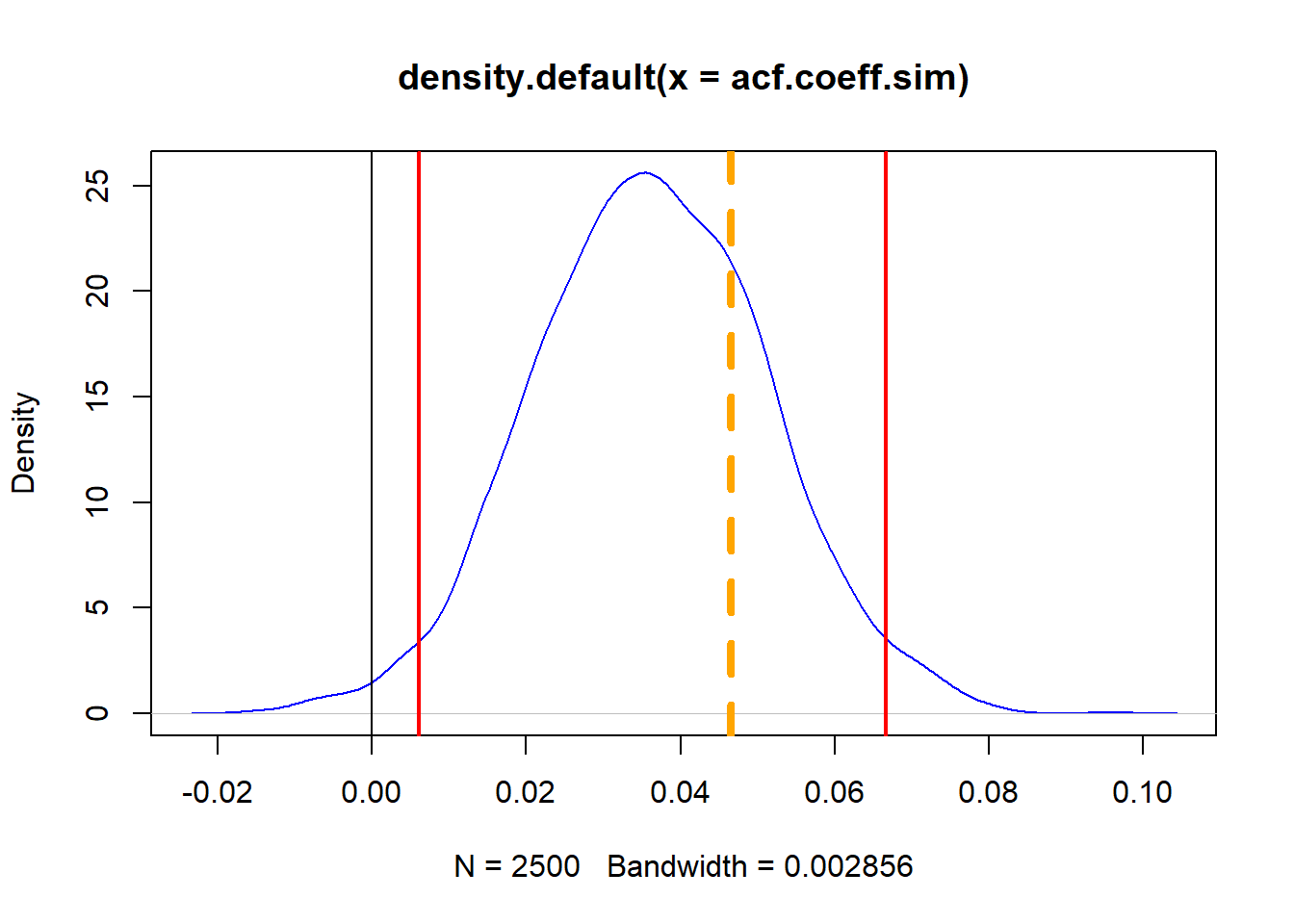
Bisakah kita menolak hipotesis nol bahwa koefisien = 0?Apakah pasar “efisien”?
- Tolak hipotesis nol karena ada peluang kurang dari 0,02% bahwa koefisiennya nol.
- Baca [Fama (2013, hlm. 365-367)] https://www.nobelprize.org/nobel_prizes/economic-sciences/laureates/2013/fama-lecture.pdf untuk diagnosis.
- Jika modelnya benar (ACF lag-1) maka pengembalian hari sebelumnya dapat memprediksi pengembalian hari ini menurut analisis kami. Dengan demikian pasar tampaknya tidak efisien.
- Ini berarti kami mungkin dapat membuat strategi perdagangan yang menguntungkan yang memanfaatkan sedikit korelasi yang kami temukan signifikan (bersih dari biaya perdagangan).
4.6 Ringkasan
Kami menjelajahi data deret waktu menggunakan ACF, PACF, dan CCF. Kami menunjukkan cara menarik data dari Yahoo!dan FRED. Kami mengkarakterisasi beberapa fakta bergaya pengembalian keuangan dan perilaku yang disimpulkan menggunakan regresi korelasi bergulir pada volatilitas. Kami kemudian menambahkan interval kepercayaan regresi kuadrat terkecil biasa menggunakan seluruh distribusi data dengan regresi kuantitatif. Kami juga membangun Menggunakan teknik bootstrap, kami mensimulasikan inferensi koefisien untuk memeriksa hipotesis pasar yang efisien. Ini, bersama dengan teknik regresi kuantil, memungkinkan kita untuk memeriksa toleransi risiko dari sudut pandang inferensi.
4.7 Bacaan Lebih Lanjut
Dalam bab ini kita menyentuh topik yang banyak dari analisis deret waktu. Ruppert et al. dalam bab 12, 13, 14, dan 15 mengeksplorasi dasar-dasarnya, seperti dalam bab ini, serta topik yang jauh lebih maju seperti GARCH dan kointegrasi.Kami akan mengeksplorasi GARCH di bab selanjutnya juga.McNeil et al. dalam bab 1 mereka mensurvei perspektif risiko, semua bantuan untuk menghasilkan apa yang disebut fakta data keuangan bergaya dalam bab 5 dan perlakuan yang lebih formal dari topik seri waktu di bab 4.
4.8 Laboratorium Praktek
4.8.1 Laboratorium praktik # 1
4.8.1.1 Masalah
4.8.1.2 Pertanyaan
4.8.2 Laboratorium praktik # 2
4.8.2.1 Masalah
4.8.2.2 Pertanyaan
4.9 Proyek
4.9.1 Latar Belakang
4.9.2 Data
4.9.3 Alur Kerja
4.9.4 Penilaian
Kami akan menggunakan rubrik berikut untuk menilai kinerja kami dalam memproduksi produk kerja analitik untuk pembuat keputusan.
- Teks ditata dengan rapi, dengan pembagian dan transisi yang jelas antara bagian dan sub-bagian. Tulisan itu sendiri terorganisir dengan baik, bebas dari kesalahan tata bahasa dan mekanis lainnya, dibagi menjadi kalimat lengkap, secara logis dikelompokkan ke dalam paragraf dan bagian, dan mudah diikuti dari tingkat pengetahuan yang diperkirakan.
- Semua hasil numerik atau ringkasan dilaporkan dengan presisi yang sesuai, dan dengan pengukuran ketidakpastian yang sesuai jika berlaku.
- Semua gambar dan tabel yang ditampilkan relevan dengan argumen untuk kesimpulan akhir. Gambar dan tabel mudah dibaca, dengan keterangan informatif, judul, label sumbu dan legenda, dan ditempatkan di dekat potongan teks yang relevan.
- Kode diformat dan diatur sehingga mudah dibaca dan dipahami orang lain. Itu indentasi, komentar, dan menggunakan nama yang bermakna. Ini hanya mencakup perhitungan yang sebenarnya diperlukan untuk menjawab pertanyaan analitis, dan menghindari redundansi. Kode yang dipinjam dari catatan, dari buku, atau dari sumber yang ditemukan online secara eksplisit diakui dan bersumber di komentar. Fungsi atau prosedur yang tidak langsung diambil dari catatan memiliki tes yang menyertainya yang memeriksa apakah kode melakukan apa yang seharusnya. Semua kode berjalan, dan file
R Markdownknitske outputpdf_document, atau output lain yang disetujui oleh instruktur. - Spesifikasi model dijelaskan dengan jelas dan detail yang sesuai. Ada penjelasan yang jelas tentang bagaimana memperkirakan model membantu menjawab pertanyaan analitis, dan alasan untuk semua pilihan pemodelan. Jika beberapa model dibandingkan, mereka semua dijelaskan dengan jelas, bersama dengan alasan untuk mempertimbangkan beberapa model, dan alasan untuk memilih satu model di atas yang lain, atau untuk menggunakan beberapa model secara bersamaan.
- Estimasi aktual dan simulasi parameter model atau fungsi estimasi secara teknis benar. Semua perhitungan berdasarkan perkiraan dijelaskan dengan jelas, dan secara teknis juga benar. Semua estimasi atau jumlah yang diturunkan disertai dengan ukuran ketidakpastian yang tepat.
- Pertanyaan substantif, analitis semua dijawab setepat yang dimungkinkan oleh data dan model. Rantai penalaran dari hasil estimasi tentang model, atau jumlah yang diturunkan, hingga kesimpulan substantif jelas dan meyakinkan. Jawaban kontinjensi (misalnya, “jika X, maka Y, tetapi jika A, maka B, selain C”) juga dijelaskan sebagai dijamin oleh model dan data. Jika ketidakpastian dalam data dan model berarti jawaban untuk beberapa pertanyaan harus tidak tepat, ini juga tercermin dalam kesimpulan.
- Semua sumber yang digunakan, baik dalam percakapan, cetak, online, atau terdaftar dan diakui di mana mereka digunakan dalam kode, kata-kata, gambar, dan komponen analisis lainnya.
4.10 Referensi
McNeill, Alexander J., Rudiger Frey, dan Paul Embrechts.2015. Manajemen Risiko Kuantitatif: Konsep, Teknik dan Peralatan. Edisi revisi. Princeton: Princeton University Press.
Ruppert, David dan David S. Matteson. 2015. Statistik dan Analisis Data untuk Rekayasa Keuangan dengan Contoh R, Edisi Kedua. New York: Springer.




